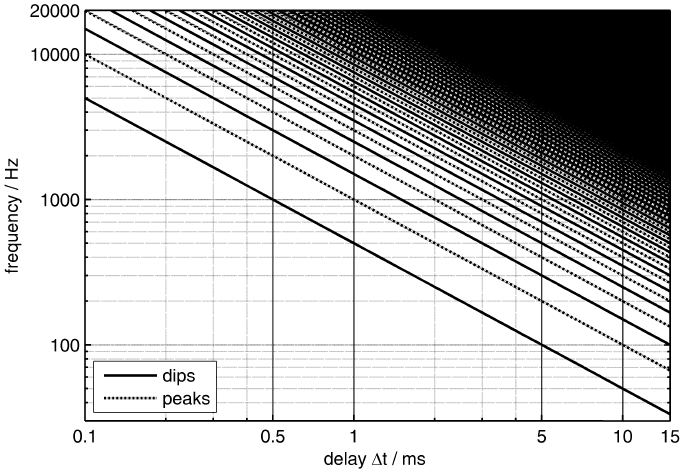Comb filter delay time dips and peaks comb filters notch frequency - initial time delay gap ITDG

● Comb filters ●
Dips and Peaks, Delay time, Interference,
and Initial Time Delay Gap ITDG

The used browser does not support JavaScript.
You will see the program but the function will not work.

First "dip" at f_n = c / 4 × d for d = λ / 2
First "peak" at f₀ = c / 2 × d for d = λ

Time delay Δ t = 2 × d / c
Speed of sound c = 343 m/s at 20°C

In psychoacoustics the terms of an echo is a reflection that comes later than the upper limit of the precedence time window and is perceived as separate auditory event. Assuming the level of reflection is as high as the original signal, then there is for clicks the limit of 8 ms, for noise it is 22 ms, for speech it is 50 ms, for music it is between 50 and 80 ms, depending on whether it's fast impulsive or slow legato music.

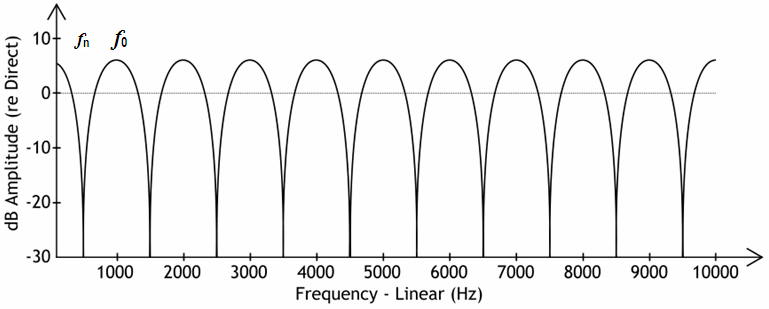
Linear representation of the frequency axis of the frequency response

Logarithmic representation of the frequency axis of the frequency response

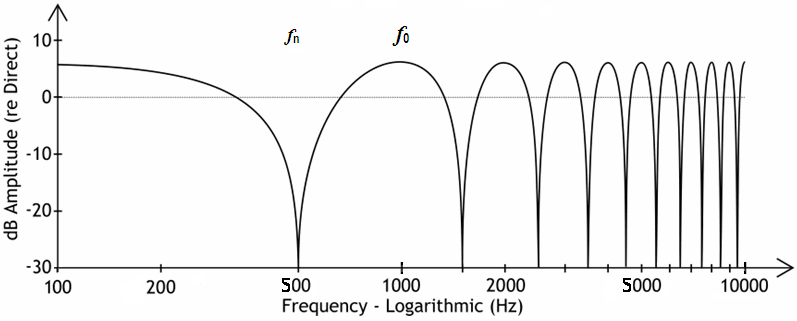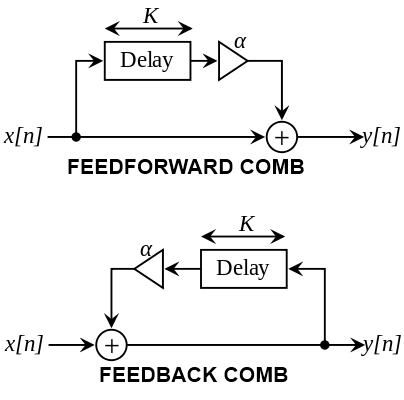
The first peak is at the frequency f₀ = c / λ = 1 / Δ t              λ = d
The first notch is at the frequency f_n = f₀ / 2 = c / (2 · λ) = 1 / (2 · Δ t)

Delay Δ t = a / c = Δ φ / (f · 360°).                           a = Distance or microphone basis
Δ t is not frequency dependent.

Phase Δ φ = Δ t · f · 360°.
Δ φ is proportional to f, that means it is frequency dependent.

Necessary microphone basis a = c / (2 · f)          c = Speed of sound c = 343 m/s at 20°C.
Phase correlation cos φ.

Frequency f = c / λ
Wavelength λ = c / f
Speed of sound c = f · λ

Comb filters are visible in the oscilloscope, but they are not always audible. In practice often unintentionally overlays with delayed signals occur - and thus comb filter effects. Room reflections in microphone recordings appearing with a delay between 2 to 15 ms can lead to abnormal, disruptive sound colorations. One should speak of "audible" comb filter effects, because only these are disturbing.
The filter notches and peaks are strongest when two signals (one is delayed) are exactly the same level, and once you're familiar with the coloured sound that comb filtering can create, you'll always recognise it when you hear it again.

Time delay Δ t and distance d (sound path)
Phase shift from time delay, time of arrival difference, and frequency

back

Search Engine

home