Sound power level SWL and sound pressure level SPL distance acoustic power sound source noiseConversion of sound pressure to sound intensity source conversion sound level energy level strength directivity factor coefficient sound source - sengpielaudio
 
Deutsche Version UK-flag s/w - sengpielaudio D-flag - sengpielaudio
 
Compare Sound power,  Sound pressure, and
Sound intensity in a distance from the sound source
 
"Sound Power Level SWL", "Sound Pressure level SPL", and "Sound Intensity Level SIL"
are different quantities which should not be confused.
 
Sound emission is defined as the sound power,
which is continuously emitted from a sound source.
The total sound energy emitted by a source
per unit time is the sound power.
 
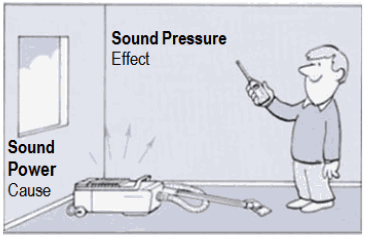
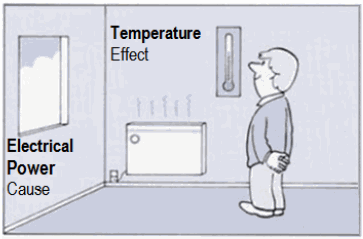
All share as level the same unit of measure: the decibel (dB). The term "sound level" is commonly substituted for each.
As characteristic impedance of air we use the round value Z = 400 N·s/m³ (Pa·s/m). Then the "sound level", that is the sound pressure level Lp and the sound intensity level LI is exactly the same as a decibel value.
The sound power or acoustic power is the sound energy constantly transfered per second from the sound source. A sound source has a given constant sound power that does not change if it is placed in a different room environment.
Sound power is a theoretical value that is not measurable. It is calculated and expressed in watts and as sound power level LW in decibels.
A sound source produces sound power and this generates a sound pressure fluctuation in the air. Sound power is the distance independent cause of this, whereas sound pressure is the distance-dependent effect.

Conversion of Sound Power Level to Sound Level

 
Sound power level (SWL) LW  dB 
Directivity factor Q   
 Distance to sound source r  m
 
             ↓
 
 Sound pressure level (SPL) Lp  dB
 
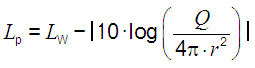Sound power level to sound pressure level
 
At r = 1 meter distance, the sound pressure level (SPL) of a point source is 11 dB less than its sound power level (SWL), when Q = 1, the full sphere propagation is given.
 
For Q = 1 (full sphere propagation) the sound power level is equal to sound pressure level or intensity level at the distance of r = 0.2821 m from the source.

Conversion of Sound Level to Sound Power Level

 
 Sound pressure level (SPL) Lp  dB 
Directivity factor Q   
 Distance to sound source r  m
 
             ↓
 
Sound power level (SWL) LW  dB
 
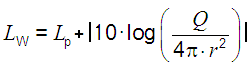Sound pressure level to sound power level
 
 
Sound power or sound power level has nothing to do with the distance from the sound source.
Thinking helps: A 100 watt light bulb is emitting constantly the same power.
That is really the case - no matter if in 1 m, in 10 m, or even in 100 distance.
These emitted watts don't change with distance. They stay in the source.
Sound power is the distance independent cause of this, whereas sound pressure is the distance-dependent effect.
 

Sound intensity, distance, and sound power at Q = 1

 
 Intensity I  W/m²   | Power Pac  W  |  Power Pac  W
   |    |  
 Distance r  m  |  Distance r   m  |  Intensity I  W/m² 
   |    |  
      ↓  |       ↓  |       ↓
   |    |  
 Power Pac  W  |  Intensity I   W/m²   |  Distance r  m
   |   Q = 1          |  
 
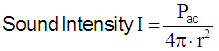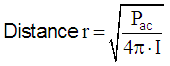Acoustic Power Formula Sound Intensity Formula Distance Formula

It is often stated that sound pressure level = SPL, sound intensity level = SIL and sound power level = SWL
are not comparable. SPL is measured in pascals = N/m2, sound intensity is energy measured in
W/m2, and sound power is measured in watts?
 
It is little known that the sound power level (without (!) distance r) is the same as the sound
pressure level and the sound intensity levelat full sphere propagation (Q = 1) at a distance
from the sound source r = 0.2821 m.
 
1 watt of sound power = 120 dB
Sound intensity at r = 0.2821 m: Pac = 1 watt / (4π × r2) = 1 watt, that means (4π × r2) = 1 and r = √(1/4π).
10 × log (1/10−12) = 120 dB
Sound pressure level SPL at 0.2821 m = SWL − (20 × log (r) − 11) = 120 − (20 × log (0.2821) − 11) = 120 dB
So how can they not be comparable?
 
The sound intensity level and the sound pressure level at a distance of 1 meter from the source
in a free field is 11 dB less than the sound power level of the source.
SIL = SPL = SWL − 11 dB or LI = Lp = LW − 11 dB.
 
Acoustic impedance of air Z0 = 400 Pa×s/m.

Sound pressure is not intensity
 
 
Differentiate: Sound pressure p is a "sound field quantity" and sound intensity I is a "sound energy quantity". In teachings these terms are not often separated sharply enough and sometimes are even set equal. But I ~ p2.
 

Changing of sound power with distance is nonsense
 
 
Important: The sound level should not be confused with sound power level! The dB values in sound pressure levels are always tied to the distance to the sound source,
however, the dB values in sound power level have really no relation to the distance from the sound source.
 
Question: How does the sound power decrease with distance"? Answer: "April fool - The sound power does not decrease (drop) with distance from the sound source."
 
However, levels of sound pressure and levels of sound intensity decrease equally with the distance from the sound source. Sound power or sound power level has nothing (!) to do with the distance from the sound source.
Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time.
Watts don't change with distance.
 
A frequent question: "Does the sound power depend on distance?" The clear answer is: "No, not really."
 
We consider sound fields in air which are described by the scalar quantity p (sound pressure) and the vector quantity v (sound velocity) as a sound field quantity.
 

zurück        start
 
Sound power and Sound power level
 
To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

 
Sound power Pac 
W		  ↔  Sound power level LW 
dB-SWL
Pac = Pac0 * 10^(Lw/10)   Formula Sound Power Level
Reference sound power Pac0 = 10−12 W ≡ 0 dB-SWL
Sound power is neither room dependent nor distance dependent.

Direct conversion of sound pressure to sound intensity and vice versa

Simply enter the value to the left or the right side.
The calculator works in both directions of the ↔ sign.

Sound field quantity   Sound energy quantity
Sound pressure p (air)
Pa		  ↔  Sound intensity I (air)
W/m2
Formel   Formel
Reference sound pressure p0 = 20 μPa = 2 × 10−5 Pa      Reference intensity I0 = 1 pW/m2 = 10−12 W/m2
Specific acoustic impedance of air Z0 = 400 N·s/m3   Sound pressure p = √ (I × Z0)   Intensity I = p2 / Z0
Sound field quantity   Sound energy quantity
Sound pressure level Lp (SPL air)
dB		  ↔  Sound intensity level LI (air)
dB
Schalldruckpegel   Schallintensitaetspegel
Reference sound pressure p0 = 20 μPa = 2 × 10−5 Pa      Reference intensity I0 = 1 pW/m2 = 10−12 W/m2
The same "sound level" in dB at Specific acoustic impedance of air Z0 = 400 N·s/m3
While the sound pressure level in the air is matched with the sound intensity level when a reference sound characteristic impedance Z0 =  400 N·s/m³ is chosen, this is not the case with the distance independent sound power level.

The same sound level at distance r = √(Q / 4π)

Geometry
 Directivity
factor Q		 Equal sound level
at distance r		 r
dB
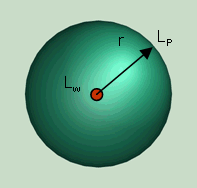
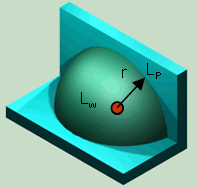
No surface near sound source; able to radiate
acoustical energy in all directions; full sphere		 1 √(1/4π) = 0.2821 m 11
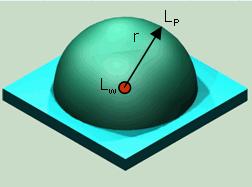
Sound source close to a flat surface; able to
radiate acoustical energy to half of a sphere (hemi) 		2 √(1/2π) = 0.3989 m 8
Close to two adjacent flat surfaces perpendicular to
each other; able to radiate to one fourth of a sphere		 4 √(1/π)  = 0.5642 m 5
At a corner; able to radiate acoustical energy to one
eighth of a sphere		 8 √(2/π)  = 0.7979 m 2

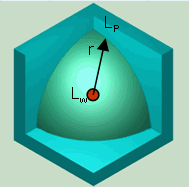Directivity Factor Full Sphere   Directivity Factor Half Sphere   Directivity Factor Quarter Sphere   Directivity Factor Eighth Sphere

Full sphere Q = 1                           Half sphere Q = 2                       Quarter sphere Q = 4              Eighth sphere Q = 8

For the practically occurring solid angle, we get the following relationships
between the sound power and sound pressure level:
For Q = 1 is LW = Lp + [20 × log10 (r)] + 11 dB (full)
For Q = 2 is LW = Lp + [20 × log10 (r)] + 8 dB (half)
For Q = 4 is LW = Lp + [20 × log10 (r)] + 5 dB (quarter)
For Q = 8 is LW = Lp + [20 × log10 (r)] + 2 dB (eighth)
Lp = medium sound pressure level at the envelope (hemispherical surface)
and for the most frequent case of radiation hemisphere r = 1 m: LW = Lp + 8 dB

Spherical Free Field Sound Propagation, Q = 1

sound pressure in distance from source

The sound pressure in a spherical distance from a source
with a known sound power can be expressed as: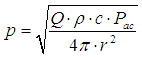
Formula Power Pressure       (1)
where
p = sound pressure in Pa = N/m2
ρ = density of air in kg/m3: 1.2041 kg/m3 at 20°C
c = speed of sound in m/s: 343.22 m/s at 20°C
Pac = sound power in W
π = 3.14159
r = distance from source in m
Q = directivity factor (spherical = 1, half spherical = 2)
directivity index - directivity factor - directivity coefficient

For a spherical sound propagation (Q = 1) at a distance of r = √(1/4π) = 0.2821 m
the decibel value of the sound pressure level is equal to the sound power level.

Hemispherical Sound Propagation, Q = 2

sound pressure in distance from source

The directivity coefficient Q depends on several parameters − the position
and direction of the source, the room or the surrounding area, etc.
The sound pressure level Lp can be expressed logarithmic as:
Lp = 20 log (p/p0) = 20 log ((Q ρ c Pac/(4 π r2))1/2/p0)
= 20 log (1/r (Q ρ c Pac/(4 π))1/2/p0)         (2)
where
Lp = sound pressure level in dB
p0 = 2 × 10−5 - reference sound pressure in Pa
Note: That for every doubling of the distance from the noise source,
the sound pressure level Lp, will be reduced by 6 decibels.

For a spherical sound propagation (Q = 2) at a distance of r = √(1/2π) = 0.3989 m
the decibel value of the sound pressure level is equal to the sound power level.

For point-like sources of sound, we get a spherical surface A.
Depending on the arrangement in space spherical segments are to consider:
Solid sphere - sound source anywhere in the room, Q = 1
Hemisphere - sound source on the ground Q = 2
Quarter sphere - sound source on the wall, Q = 4
Eighth sphere - sound source in the corner, Q = 8
Q = directivity factor and the area A = (4π × r2) / Q

Sound intensity I = sound power Pac / area A
Sound power Pac = I × A = I × 4π × r2.

Sound Pressure Level Calculator

Consider a source of sound and imagine a sphere with radius r, centered on the source.
The sound source outputs a total power P, continuously. The sound intensity I is the same
everywhere on this surface of a thought sphere, by definition. The intensity I is defined as the
power P per unit area A. The surface area of the sphere is A = 4π × r2, so the sound intensity
passing through each square meter of surface is, by definition:
I = P / 4π × r2.
We see that sound intensity is inversely proportional to the square of the distance away from
the source (1/r2):
I2 / I1 = r12 / r22.
But sound intensity is proportional to the square of the sound pressure, I ~ p2, so we can
write:
p2 / p1 = r1 / r2. The sound pressure p changes with 1 / r of the distance.

So, if we double the distance, we reduce the sound pressure by a ratio of 2 and
the sound intensity by a ratio of 4: in other words, we reduce the sound level by
6 dB. If we increase r by a ratio of 10, we decrease the level by 20 dB.

When a point source emits sound (or an other form of energy) uniformly in all directions in a free field, it is spreading over the surface of a sphere of increasing radius. Full sphere area is 4π × r². Directivity factor Q = 1.
The same amount of energy is spreading over a larger and larger area, therefore, the intensity will decrease.
The sound source is emitting all the time the acoustic power and stays there. The sound power does not decrease with the distance from the sound source.

Converting sound power level to sound pressure level

A noise source radiates power which is measured as the sound power level.
It is a characteristic of the source alone and is independent of distance. It is used to rate and compare different noise sources. The sound pressure level of the source is the level of sound caused by the source but at a distance from it.
The level of sound pressure is therefore distance dependent.
The level of sound power is not distance dependent.
The formula for converting sound power level to sound pressure level:
Lp = LW − 10 × log (Q / 4π × r²) in dB
For Q = 1 is SWL = SPL + [20 × log10 (r)] + 11 dB
For Q = 2 is SWL = SPL + [20 × log10 (r)] + 8 dB,
where
Sound pressure level = SPL or Lp in dB,
Sound power level = SWL or LW in dB,
Distance from the source to the measuring point = r.

W. T. W. CORY: "Relationship between Sound pressure and Sound Power Levels"

 
Power is like all energy quantities primarily a calculated value.
 

"Sound power" and "sound pressure" are two distinct and commonly confused characteristics of sound. They have a cause and effect relationship. Sound power is the acoustical energy emitted by the sound source, and is an absolute value. It is not affected by the environment. Sound power levels are connected to the sound source and are independent of distance. Sound power levels are indicated in decibels.
Lw = 10×log (P / P0) where:
The reference power is 10−12 watts (W), which is the lowest sound persons of excellent hearing can discern. Sound power is measured as the total sound power emitted by a source in all directions in watts (joules per second).
 
Since sound measuring instruments respond to sound pressure the "decibel" is generally associated with sound pressure level (SPL). Sound pressure levels quantify in decibels the strength of given sound sources. Sound pressure levels vary substantially with distance from the source, and also diminish as a result of intervening obstacles and barriers, air absorption, wind and other factors.
Sound pressure levels are indicated in decibels. Sound pressure level (SPL) is
Lp = 20×log (p / p0), where:
The reference sound pressure is p0 = 2×10−5 Pa = 20 µPa. Sound pressure is a pressure disturbance in the air whose intensity is influenced not only by the strength of the source, but also by the surroundings and the distance from the source to the receiver. Sound pressure is what our ears hear and what sound pressure level meters (SPL meters) measure.
 
 
 
back zurück Search Engine weiter home start