Deutsche Version

Cut-off frequency:

Time constant:

Conditional equations:
Cut-off frequency f_c in Hz = 159155 / τ in µs
Time constant τ in µs = 159155 / f_c in Hz

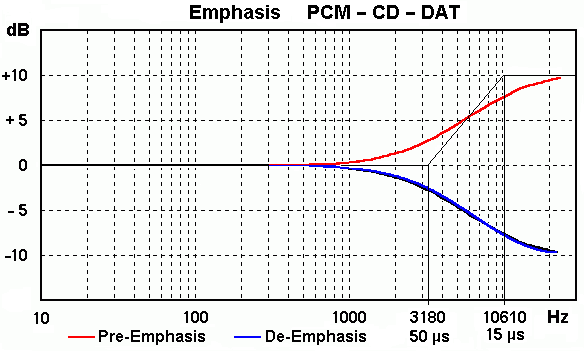The possible pre-emphasis/de-emphasis of a PCM recording for DAT or CD (15/50 µs EIAJ DAT/CD).

Cut-off frequency:

Time constant:

Conditional equations:
Cut-off frequency f_c in Hz = 159155 / τ in µs
Time constant τ in µs = 159155 / f_c in Hz

At the cut-off frequency fc of a drop, the voltage V is always fallen to the value of 1/√2 and the voltage level is damped to 20 × log(1/√2) = (−)3,0103 dB.

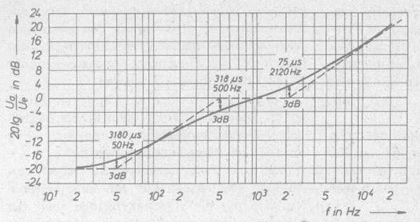
Time constant and cut-off frequency

AME - Ampex Master Equalization Curve
Pre-Emphasis and De-Emphasis or preemphasis and deemphasis

There was also an "Ampex Master Equalization" around the year 1958, called AME. It was based on modifying the NAB response with an auditory (hearing) curve, which resulted in a recorded flux that had a "hump" (re the NAB EQ) from about +3 dB at 630 Hz to +8 dB at 2 kHz, back to +3 dB at 5 kHz, and down to −12 dB at 16 kHz; see the AME curve: http://home.comcast.net/~mrltapes/pubame.pdf http://www.richardhess.com/tape/ame_equalizer_20040412.pdf

In USA FM radio has a time constant of 75 µs, but also in Korea, Taiwan, Thailand, AFN worldwide and the rest of America. In Europe FM radio has a time constant of 50 µs, but also in Africa, Asia (without Korea, Taiwan, Thailand), Pacific.

Record RIAA cutting equalization  

Conversion  

To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign.

Cut-off frequency fc  Hz	↔	Time constant τ   µs
1 microsecond = 10−6 second = 0.000001 second

Time constant τ = R × C            R = τ / C            C = τ / R

Time constant in seconds = Resistance in ohms × Capacitance in Farad

Please enter two values, the third value will be calculated.

Time constant τ  microseconds  Resistance R  ohms Capacitance C  microfarad

Corner angular frequency ωc = Angular frequency ωc The corner angular frequency ωc is developed from the corner frequency fc: ωc = 2 π × fc Corner frequency fc = Cut-off frequency fc For systems that correspond to a differential equation of first grades the cutoff point is the intersection of the horizontal asymptote with the asymptote of the falling branch of the Bode diagram. At this point, the level is −3 dB and the phase shift is 45°. This means that the amplitude drop of the output value reached 30% of the input size. At the same time the time constant τ of such system is: τ = 1 / ωc = 1 / 2 π × fc

Cut-off frequency to corner angular frequency and vice versa  

To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign.

rad = radiant
Cut-off frequency fc  Hz	↔	Corner angular frequency ωc  rad/s

Conversion of dB/octave to dB/decade
dB/oct to dB/dec

The increase of 20 dB per decade is equivalent to the increase of 6 dB per octave

6 dB/octave = 20 dB/decade 12 dB/octave = 40 dB/decade 18 dB/octave = 60 dB/decade 24 dB/octave = 80 dB/decade 20/6.0206 = 3.3219 There are 3.322 octaves in 1 decade, so 1 dB/decade = 3.322 × dB/octave.

 

To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign.

dB/octave	↔	dB/decade
acoustics		physics

 

back

Search Engine

home