Standing waves are stationary waves room modes acoustic resonance on strings string vibrations room modes sound pressure level between hard parallel walls node antinode particle displacement sound pressure stationary room acoustic frequency - sengpielaudio
 
Deutsche Version UK-flag s/w - sengpielaudio D-flag - sengpielaudio
 
● Room Modes ●
 
Standing waves are called room modes at sound reflecting hard parallel walls.
 
The table below summarizes the features of the standing wave of sound in air as sound pressure p for the first harmonics between two hard reflecting walls. Sound technicians should know this.
The 1st harmonic is the fundamental frequency of the standing wave.
 
 Harmonics 
Number
of
Nodes
Number
of
Antinodes
Sound pressure
Patterns
Room walls
Length
 Relationship 
1st
1
2
Harmonic 1
L = 0.5 · λ
2nd
2
3
Harmonic 2
L = 1 · λ   
3rd
3
4
Harmonic 3
L = 1.5 · λ
4th
4
5
Harmonic 3
L = 2 · λ   
5th
5
6
Harmonic 5
L = 2.5 · λ
6th
6
7
Harmonic 6
L = 3 · λ   
nth
n
n + 1
---
L = (n·λ)/2
 
Standing waves and acoustical resonance. Vibrations of strings are no room modes.
 
The table below summarizes the features of the standing wave as particle displacement ξ for the first several harmonics of a clamped string, which must be fixed at the two end points.
 
 Harmonics 
Number
of
Nodes
Number
of 
Antinodes
  Displacement  
Patterns
String
Length
 Relationship 
1st
2
1
Harmonic 1
L = 0.5 · λ
2nd
3
2
Harmonic 2
L = 1 · λ   
3rd
4
3
Harmonic 3
L = 1.5 · λ
4th
5
4
Harmonic 4
L = 2 · λ   
5th
6
5
Harmonic 5
L = 2.5 · λ
6th
7
6
Harmonic 6
L = 3 · λ   
nth
n + 1
n
---
L = (n·λ)/2
 
In the figure on top the sound pressure of a sine wave with harmonics is presented between two totally reflecting walls which in reality is a longitudinal wave.
It is important that in the case of resonance there is always a maximum sound pressure on the walls. In many figures this is wrongly shown as a vibration of a string, which has always a fixed node (knot) at each end, as in the following example:
 
This is not the representation
of sound pressure vibrations
between walls in a small room.

These are vibrations of a string 
(displacement amplitudes).		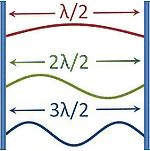 Wrong Room Modes  A typical wrong figure with
 nodes at the wall.

 Showing the air displace- 
 ment is not wanted.
 
A string is clamped between two "fixed ends". At the ends will be a wave node.
A wave between two hard walls is considered as a sound pressure with "loose ends".
Therefore on the sides of the wall there appears as sound pressure a wave maximum or an antinode.

Sound technicians are looking at room modes only for the amplitude of the sound pressure p (sound pressure amplitude), because this quantity moves our eardrums and let us hear the disturbing low-frequency room modes. Not interesting is the amplitude of sound displacement ξ (amplitude of the air particle deflection), the amplitude of the particle velocity v, and the amplitude of the pressure gradient Δ p; see: "What is an amplitude?" and "Soundfield Quantities of a Plane Wave − The Amplitudes".
 
 
Note, because there is often confusion:
An antinode in sound pressure (pressure antinode) is at the same time a node in the displacement of the air particles (particle displacement node).
The problem is that it is mostly forgotten to tell the viewer of the figures what they see: sound pressure variations or motion of particle displacement.
 
 
Room modes as sound pressure deviations (left) or as particle displacement of air (right)?
 
Room modes - Sound pressure or particle displacement
 
The formation of standing sound waves in air at sound hard walls (room modes) has to be distinguished from the vibrations of a string between two clamped points.
 
Conclusion: The requirement for a room mode is a standing wave, but standing waves must be no room modes.
 
For an oscillatory system it is generally applicable that the amplitude, or more precisely, the sound pressure amplitude is much more pronounced when the excitation is performed with an eigenfrequency of the system. This special case is generally referred to in physics as a resonance, see:
 
"Standing waves (acoustic resonance) on ideal strings":
http://www.sengpielaudio.com/StandingWaves.htm
 
"Calculation of the three room modes of rectangular rooms":
http://www.sengpielaudio.com/calculator-roommodes.htm
 
A sound wave is reflected back and forth between two parallel walls. At a given wavelength λ = 2 × L (L = room length, width or height) both waves fit exactly superimposed und deliver a full standing wave. If the distance of the parallel walls is just a multiple of the half wavelength, there are 'standing' waves, which is a sound pressure increase.The frequency at which this happens, is called resonant frequency or room mode.
 
At frequencies that are not a multiple of this frequency, the sound pressure maxima are located at different locations, whereby the effects partly cancel and standing waves are small or even extinguish. In practice, only low frequencies below 300 Hz are heard as room modes. Higher modal frequencies become less important because their interference effect is masked by other room acoustic effects. Close to reflective walls modes always show up that are sound pressure maxima - which are antinodes when you think of the important sound pressure deviations.
 
Wrong Room Modes
Courtesy: www.classroom.com
 
 
 
back back Search Engine forward home start