

| Deutsche Version |
 |
 |
 |
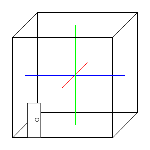
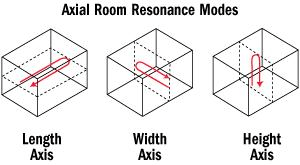
| The axial, tangential, and oblique room modes of rectangular homogeneous rooms are computed. Axial room modes hit on two facing surfaces. Tangential room modes hit on four surfaces and oblique room modes include six surfaces crosswise. Thus one can find the optimal room dimensions for home cinemas, control rooms, sound studios, and exercise rooms. The distribution of the modal frequencies should be as homogeneous as possible. |
 |
Notice: Only low frequencies up to 300 cycles per second are to be regarded. Higher modal frequencies lose their meaning, because the interfering effect is covered by other room acoustic effects. In audio technology we consider at reflecting walls only the modes as sound pressure maxima - that are disturbing antinodes. |
| Theory is good, but it shows up: An empty room can be computed marvelously, but afterwards
the brought in mixer, the couch, the cabinets, the racks, and the shelves for the effect devices
destroy the nice computations e.g. for a control room. Such is practice. Rectangular spaces room modes can be easily predicted from the length, wide and height dimensions. If you have a non-rectangular or odd shaped room (e.g. L-shaped or open plan) then a calculation is a problem. Eric Desart, a Belgian acoustican, tells us, that this calculator shows not all eigenfrequencies. Therefore this calculator is not to use for scientific calculations. If you look for another program you can try the Room Modes Calculator by Bob Golds or also: Amroc - The Room Mode Calculator. In all parts of the audible spectrum there will be room modes, but whether or not they will be appreciable as colorations depend on the following factors: a) the bandwidth of the mode b) the degree of excitation of the mode c) its separation from neighboring strongly excited modes d) the positions of the sound source and microphone with respect to standing-wave systems e) the frequency content of the sound source |
 |
 |
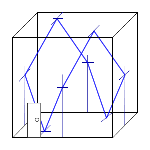
antinodes | nodes | wavelength | frequency | harmonics | overtones |
| 2 | 1 | λ = 2 L | f1 = c / (2 L) | 1st harmonic | fundamental frequency | |
| 3 | 2 | λ = L | f2 = 2 × c / (2 L) | 2nd harmonic | 1st overtone | |
| 4 | 3 | λ = (2 / 3) × L | f3 = 3 × c / (2 L) | 3rd harmonic | 2nd overtone | |
| k + 1 | k | λ = (2 / k) × L | fk = k × c / (2 L) | k harmonic | (k – 1) overtone |
 |
| "Room Mode calculator" – Courtesy of: Mc Squared System Design Group, Inc. |
|
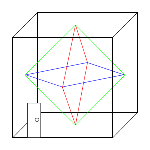
*) The three graphics above: Courtesy of Brüel & Kjær – Technical Review.
To calculate the frequencies of the axial, oblique and tangential modes, use the following equation: 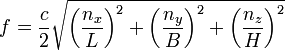 f = Frequency of the mode in Hz c = Speed of sound 343 m/s at 20 °C (68 °F) nx = Order of the mode of the room length ny = Order of the mode of the room width nz = Order of the mode of the room height L, B, H = Length, width, and height of the room in meters |
| The number of modes per frequency width Δ f and even more per frequency interval of Δ f / f increases with rising frequency. Problems with inhomogeneities through in the spectrum clearly separated natural oscillations arise thus particularly in small rooms and at low frequencies. Eigenoscillations arise not only in rectangular rooms, but also in skew rooms. They can be determined there however no longer as simply as here computed, but must be calculated by numeric procedures. An even mode distribution over the frequencies can be reached only by favorable room proportions, especially the eigenfrequencies of different room dimensions should not fall together. Favorable distributions result for proportions (standardized H = 1 on the height) like: (H/B/L). |
| Height H | Width B | Length L | |
| A | 1.00 | 1.14 | 1.39 |
| B | 1.00 | 1.28 | 1.54 |
| C | 1.00 | 1.60 | 2.33 |
| Note, because there is often confusion: An antinode in sound pressure (pressure antinode) is at the same time a node in displacement of the air particles (particle displacement node). The problem is that it is mostly forgotten to tell the viewer of the figures what they see: sound pressure p variations or motion of particle displacement ξ. |
Room Modes (Sound Pressure Level – SPL)
 |
| You see the level of the sound pressure and not the level of the particle displacement of the air. At the walls you find the maximum sound pressure level (antinode). |
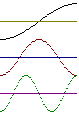
| There is no room correction by setting EQ. The notion of using EQ to fix bad room response is mostly misguided. In some cases EQ can help only "a little bit" to tame modal peaks at the very lowest frequencies. But most low frequency response errors are highly position dependent, and include nulls as deep as 30 dB. So any EQ correction will help only one very specific place in the room, and will by definition make other places worse. Even a foot away the response can be very different. And EQ does nothing for other acoustic problems like first reflections, flutter echo, modal ringing, and so forth. You are doing only a "correction of the loudspeaker frequency response" and not a positive "room correction" for all listening places. EQ systems are not normally used to create a perfect inversion of the room's response because a perfect correction would only be valid at the location where it was measured. A few centimeters away the arrival times from various reflections will differ and the inversion will be imperfect. The imperfectly corrected signal may end up sounding worse than the uncorrected signal because the acausal filters used in digital room correction may cause pre-echo. |
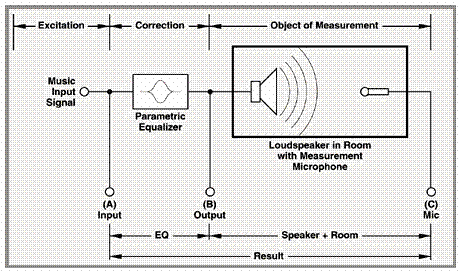
| Measurement of a loudspeaker in a room and correction by a parametric equalizer. You find here the loudspeaker frequency response correction – and no "room correction". The time delay between loudspeaker and measuring point is often overlooked. |
| An equalization cannot be a substitute for good acoustics. |
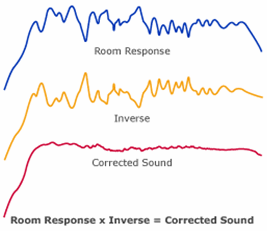 |
You can never get this corrected curve for all parts of the room.
Standing waves in strings, and room modes between hard parallel walls
Room modes - Standing waves in air - Bass reflections at walls
Room Modes and Vibrations of Strings
| back |
Search Engine |
home |