Parallel Resistor Calculator R1 + R2 = equivalent resistor R resistance circuit equiv total resistor finder made easy piggyback = parallel

● Calculate Resistors in a Parallel Circuit ●

Parallel Resistance Calculator

Parallel Resistor Finder - Piggyback means in parallel and not in series.

Calculation: Rtotal and Parallel Resistors R1 or R2

Formula for resistors in series: R_total = R₁ + R₂ + R₃ + ...

The used browser does not support JavaScript.
You will see the program but the function will not work.

R_total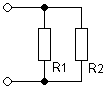

Formula:
R_total = R1×R2/(R1+R2)

Please enter two resistor values, the third value of the parallel circuit will be calculated.
You can even enter the total resistance R_total and one known resistance R₁ or R₂.

Formula (equation) for the calculation of two resistances R₁ and R₂ connected in parallel:

Calculation of the necessary parallel resistor R₂, when R₁ and the total resistance R_total is given:

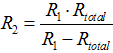
Formula resistor parallel

Solving the formula R_total= (R₁× R₂) / (R₁ + R₂) for R₁:
The first step is to clear all fractions by multiplying by the lowest
common denominator, that is R_t × R₁ × R₂ ... so we get:
1/R_total = 1/R₁ + 1/R₂
R_total × R₁ × R₂[1/R_total = 1/R₁ + 1/R₂]
R₁ × R₂ = R_total × R₂ + R_total × R₁ then collect terms with R₁ and solve
R₁ × R₂ − R_total × R₁ = R_total × R₂
R₁(R₂ − R_total) = R₂ × R_total
Last step:
R₁ = R₂× R_total / (R₂ − R_total)
or:
R₂ = R₁ × R_total/ (R₁ − R_total)

Notice: This calculator can also solve other math problems. Calculating resistors in parallel is
precisely the same as the calculations required for inductors in parallel or for capacitors in series.

Two resistors in parallel and the resulting total resistance: Two of the same value,
also show the equation that the results are always half. That makes it easier when
designing circuits or prototyping. With caps it's always double, then again caps just
simply add up in parallel.

• Search resistances R₁ and R₂, when the target resistance (equivalent resistance) is known •

Calculation: Resistor pairs - reverse engineered calculator
Search of R₁ and R₂ with known target resistance

● Calculate many resistors in parallel ●

This calculator determines the resistance of up to 10 resistors in parallel.
Enter resistances into the boxes below and when all values have been input,
click on the 'calculate' button and the result will appear in the box below that button.
As a test, if we enter resistances of 4, 6, and 12 ohms, the answer should be 2 ohms.
Notice: Manually clearing the boxes does not reset stored values. Use "reset".

Ohm's law - calculator and formulas

Two resistors in parallel and the resulting total resistance
Resistance ranging from 1 ohm to 100 ohms

R2	R1
R2	1	1.5	2.2	3.3	4.7	6.8	10	15	22	33	47	68
1	0.5	0.6	0.69	0.77	0.83	0.87	0.91	0.93	0.95	0.97	0.98	0.99
1.5	0.6	0.75	0.89	1.03	1.14	1.22	1.30	1.36	1.40	1.43	1.45	1.46
2.2	0.69	0.89	1.1	1.32	1.50	1.66	1.82	1.92	2.0	2.06	2.10	2.13
3.3	0.77	1.03	1.32	1.65	1.94	2.22	2.48	2.70	2.87	3.00	3.08	3.14
4.7	0.83	1.14	1.50	1.94	2.35	2.78	3.20	3.58	3.87	4.12	4.27	4.39
6.8	0.87	1.22	1.66	2.22	2.78	3.40	4.05	4.68	5.19	5.64	5.94	6.18
10	0.91	1.30	1.82	2.48	3.20	4.05	5.0	6.0	6.9	7.7	8.3	8.7
15	0.93	1.36	1.92	2.70	3.58	4.68	6.0	7.50	8.9	10.3	11.4	12.2
22	0.95	1.40	2.00	2.87	3.87	5.19	6.9	8.9	11.0	13.2	15.0	16.6
33	0.97	1.43	2.06	3.0	4.12	5.64	7.7	10.3	13.2	16.5	19.4	22.2
47	0.98	1.45	2.1	3.08	4.27	5.94	8.3	11.4	15,0	19.4	23.5	27.8
68	0.99	1.46	2.13	3.14	4.39	6.18	8.7	12.2	16.6	22.2	27.8	34.0

Power dissipated in resistor: P = V × I, P = V² / R, P = I² × R.

Notice: For resistors in series, the current is the same for each resistor,
and for resistors in parallel, the voltage is the same for each resistor.

back

Search Engine

home