Efficiency and sensitivity conversion - loudspeaker percent and dB per watt and meter loudspeaker efficiency versus sensitivity vs speaker sensitivity 1 watt = 2,83 volt box chart

● Loudspeaker efficiency versus sensitivity ●
Loudspeaker efficiency and loudspeaker sensitivity level are not the same.

Conversion of sensitivity level in dB per 1 watt and a distance of
1 meter to energy efficiency in percent for passive loudspeakers
For an 8 ohm loudspeaker, the voltage of 2.83 volts produces exactly 1 watt.

A loudspeaker converts electrical power to acoustical power
An "acoustic amplifier" is called "loudspeaker".

The used browser does not support JavaScript.
You will see the program but the function will not work.

In loudspeaker data you never see the real efficiency in percent,
but usually you find the sensitivity in dB per 1W in 1m distance instead.

You will get a shock if you know how inefficient the conversion of the electrical power
P_e of the amplifier to the emitted (acoustical) sound power P_ac of the speaker really is.
The efficiency is only around 2 percent.

Efficiency is not the same as sensitivity.

− but it is possible to convert efficiency to sensitivity and vice versa:

Sensitivity in dB = 112 + 10 log (efficiency)

Efficiency = 10^{(Sensitivity in dB – 112)/10}

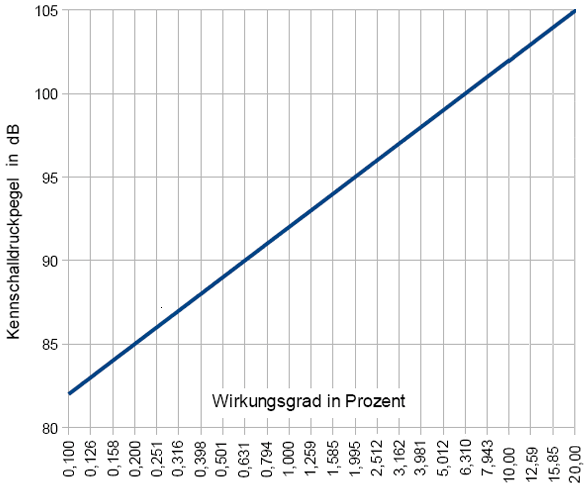
Loudspeaker data
Efficiency	Percent	Sensitivity
0.2	20 %	105 dB
0.1	10 %	102 dB
0.05	5 %	99 dB
0.02	2 %	95 dB
0.01	1 %	92 dB
0.005	0.5 %	89 dB
0.002	0.2 %	85 dB
0.001	0.1 %	82 dB

105 dB is very efficient and 82 dB is very inefficient

Kennschalldruckpegel und Wirkungsgrad in Prozent

The sensitivity of a loudspeaker is the sound pressure between 125 Hz (250 Hz) to
4 kHz (8 kHz) at a specific distance - when you have a constant voltage - measured in dB per watt and meter. 2.83 volts = 1 watt into an 8 ohm load (nominal impedance) at a distance of
1 metre. Mostly it is the voltage of constant 2.83 volts at the distance of 1 meter, at 8 ohms nominal impedance. Herewith is the power P = V ² / R = 2.83² / 8 = 1 watt. With a 4 ohms loudspeaker you generate 2 watts. To get the reference value of 1 watt, you have to subtract from the sensitivity 3 dB.
It is not the efficiency you get here, it is the sensitivity.
The very small value of the efficiency is never shown by a manufacturer. Usual values for HiFi speakers and studio monitors are between 0.2 % and maximum 2 % − that is an efficiency of 0.002 to 0.02.
There is no connection between the efficiency and the sound quality.

Efficiency

The efficiency of a system is defined as the ratio between the useful delivered power output divided by the input power, denoted by the Greek letter small eta (η).
It has to be destinguished between the electrical power P_e
of the amplifier and the emitted sound power of the speaker P_ak.

Acoustic efficiency η (eta) of a loudspeaker is:

Please note that speakers do not produce power, amplifiers do. A loudspeaker rated at 1000 watts is not necessarily going to be more efficient than a speaker rated at 50 watts.

Where does the 112 dB come from? The 0 dB reference level for sound is 10⁻¹² watts.
1 acoustical watt means 120 dBSPL.
The standard measurement for loudspeakers is done with an infinite baffle sounding in a half room with a distance of r = 1 m.
The resultant factor 2π × r² (area of a half sphere) equals −8 dB. Therefore we get for an efficiency of 1 = 100 % a sensitivity of 120 − 8 = 112 dB.

This calculation works correct if the loudspeaker radiates in a hemisphere 2π. Otherwise you must add the factor Q because of directionality.
Solid sphere Q = 1, hemisphere Q = 2, quarter sphere Q = 4, and eighth sphere Q = 8.

Many car and disco freaks need for their huge loudspeakers:
The Big Power Formulas
Electrical and mechanical power calculation.

To get a high loudness from loudspeakers you should know:
How many decibels (dB) is twice (double, half) or three times as loud?

Studio monitors have a small energy efficiency around 1 %, but that gives a very high uncolored sound quality.

If you are looking for big party loudspeakers with high efficiency you have really to think of impedance matching (power matching) and megaphones. They have always an efficiency of more than 10 %, but with the well known distortions and giving a strange colored sound. That comes really through and has "pressure" and you can hear the "power".
Megaphon - high efficiency

If you need even more efficiency you have to think of a siren on emergency vehicles.
But the frequency bandwidth is very limited.

Extremes:
dB Drag Racing (racer) is a competition rewarding the person who can produce the loudest sound inside a vehicle with a car's sound system. Current world record is over 177 dB SPL. These audio gear does not play usual wideband pop music, like black metal or gangsta rap, but a single (!) audio frequency. Only by this way an extremely high efficiency can be achieved; see emergency horn.

Typical Question: Calculate the maximum sound pressure level of a loudspeaker in 1 m
distance, when the sensivity level of 98 dB/1W/1m is given and the wattage is 300 W.
Answer: At 1 Watt you get 98 dBSPL in 1 m distance. At 300 W there is:
10 × log 300/1 = 24.77 dB more level, that means 122.77 dBSPL.

Sometimes the efficiency is given in decibel instead of percent.

Simply enter the value to the left or the right side.
The calculator works in both directions of the ↔ sign.
The damping value in dB must begin with a minus sign.

Decibel to Percentage Converter

Decibel Table - Comparison Chart - dB Scale

Loudspeaker:
Sound pressure level and amplifier power

A sound pressure increase of approximately 10 dB is considered as a doubling of the volume.

A doubling of the listening distance from a loudspeaker gives a reduction of sound pressure by 6 dB. In practice, that is in a room with hard walls, the sound pressure reduction is less. A doubling of the number of loudspeakers is an increase of sound pressure by 3 dB.

Electro-acoustic sensitivity

The electro-acoustic sensitivity for sound transmitters, so for speakers. Size to indicate the frequency range that can transmit a reversible transducer. For a speaker as a sound generator it is the electro-acoustic transmission factor, the ratio of radiated sound pressure at 1 m from the transducer on the applied voltage.

Electroacoustic transfer factor B_s = p_r / V in Pa/V
B_s = Electroacoustic sensitivity of the transmitter in Pa/V
p_r = Sound pressure Pa at a distance of r = 1 m
V = Voltage at the speaker, reference sensitivity for sound sources:

Reference electroacoustic sensitivity B_s0 = 0.1 Pa/V

Does the usual word "loudness" actually mean the volume level, the loudness level, the sound pressure level, the proportional voltage level, the sound intensity level, the sound power level, the sound energy density level, or even the A- weighted or C-weighted sound?
This is about the level dynamics of the amplitudes.
The subjectively perceived loudness is a term of psycho-acoustics, which describes the strength of the perception of sound through our ears. This is not easy to understand. The loudness of a sound is expressed in sones. The volume level of a noise is specified in Phon. The loudness of 1 sone corresponds to the volume level 40 phon, or 40 dB SPL at a 1000 Hz pure tone.
The poet Kurt Tucholsky said: "The own dog does not make noise - it only barks." and "Noise is the sound of others."

back

Search Engine

home


Percent value k %	↔	Damping value a_k dB
k = THD
100 percent = 1 ≡ 0 dB