

| Deutsche Version |
| This is not a trick question. This is not about the subjective perceived loudness of hearing
and not how to add sound sources. SPL is the abbreviation for "Sound Pressure Level".
The term loudspeaker and amplification is not specifically raised with the previous survey.
It's all about sound pressure the most important sound value. There is only one correct answer: Twice the sound pressure is an SPL of +6 dB. We should go on reading, if we want to know more and want to understand all this stuff. |
| Subjectively perceived loudness (volume), objectively measured sound pressure (voltage), and theoretically calculated sound intensity (acoustic power) |
| You will find here the dependence of sound levels in dB, the respective factors, and evaluation of measurements and personal perceptions. |
| It's not easy to understand the relationship between these terms: There
is the subjectively and artificially perceived concept of loudness, the
objectively measurable audio voltage from a microphone which is
proportional to the sound pressure (a sound field size) and last, but
not least there is the calculated sound intensity (acoustic strength) or
acoustic power (a sound energy size). How many decibels (dB) is twice (double, half) or three times as loud? Loudness/Volume − What is the dependence of the level in decibels? What does the common phrase "sound level" mean? Is it the volume level, the loudness level, the sound pressure level − thus proportional to the voltage level, the sound intensity level, the sound power level − or does it mean the A-weighted or C-weighted sound level? This is about the level dynamics of the amplitudes. |
It's often necessary to estimate how much a sound level changes. Our ears interpret a wide
range of sound amplitudes, volume or loudness as change in level and change in loudness.
The decibel is a very convenient unit for measuring signal levels in electronic circuits or
sound pressure levels in air. However, changes in the loudness of sounds as perceived by
our ears do not conform exactly to the corresponding changes in sound
pressure level. Loudness is the quality of a sound that is the primary psychological correlation of physical
strength (amplitude). Loudness, a subjective feeling, is often confused with objective
measures of sound pressure level SPL such as decibels. |
| A person feels and judges sound events by exposure time, spectral composition,
temporal structure, sound level, information content and subjective mental attitude.
Three physically measurable parameters can be identified and separated from each other in
musical material and can be described as the pitch (or fundamental frequency f), the tone
duration (or time interval Δ t), and the
volume (or amplitude y0). Sometimes, even the timbre or the acoustic spectrum representing the number and relative strength of overtones is regarded as one of the parameters. However, "timbre" can only count as a parameter in a figurative sense, because it does not consist of a variable with a discrete value. Never forget the change of volume caused by the distance between the source of sound and the listener. A typical question: "How many more times "intense" would the 18 dB sound seem compared to the 6 dB sound?" The level difference is 18 dB minus 6 dB = 12 dB. The calculator answers: 12 dB level difference equals a sound intensity factor of 15.85 or a sound pressure factor of 3.98, or a loudness factor of 2.3. Do we know what intensity means? Do we really need this intensity? Doubled loudness (volume) is how many dB? Really loudness? |
| Avoid using the psychoacoustical terms loudness perception and volume. This subjective sound-sensation is not clearly measurable without ambiguity. The term "loudness" or "volume" is a problem because it belongs to psycho- acoustics and this personal feeling is not correct definable. Loudness as a psychological correlate of physical strength (amplitude) is also affected by parameters other than sound pressure, including frequency, bandwidth, spectral composition, information content, time structure, and the duration of exposure of the sound signal. The same sound will not create the same loudness perception by all individuals (people). |
| As psycho-acoustic parameters to describe the "loudness" there is the "loudness level" with the unit phon and the "loudness" with the unit sone. |
Levels in decibels (dB) and their different factors
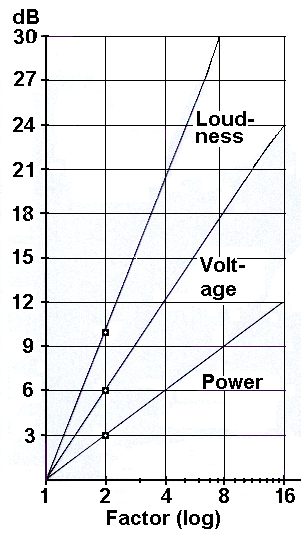 |
| Double or twice the loudness = factor 2 means about 10 dB more sensed loudness level (psycho acoustic) Double or twice the voltage = factor 2 means 6 dB more measured voltage level (sound pressure level) ● Double or twice the power = factor 2 means 3 dB more calculated power level (sound intensity level) |
| While every 6 dB SPL represents a doubling of amplitude, a non-exact rule-of-thumb is that every 10 dB increase is a doubling of perceived loudness - psycho-acousticians tell us. Don't use the term "doubling of decibels, or doubling of dB". Always the factor is doubled. |
Sound level change and loudness ratio
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| The ratio (factor) is in mathematics part of a product. A ratio is x times the increase of a basic value.
Loudness or volume are not the same as intensity. Aha, that is a light bulb moment. The sound wave's amplitude (RMS) is the fluctuation in sound pressure as the wave passes by. |
| "Loudness" cannot be the same as "intensity" and
"sound intensity" is not the same as "sound pressure". Distinguish clearly between loudness, sound pressure, and (sound) intensity. And what is amplitude? |
| When talking about sound as heard by our ears or by microphones, take care to speak in terms of sound pressure as sound field quantity. The sound energy measurements such as sound intensity and sound power have not much use here and are mostliy misleading. Air pressure fluctuations considered desirable such as speech or music are pleasant to the ear, while undesirable ambient sound such as traffic noise is anoying. |
Twice, two fold, and doubling sound . . .
Which sound?
| Doubling of the volume (loudness) should be sensed as a level difference of +10 dB − acousticians say. Doubling the sound pressure (voltage) corresponds to a measured level change of +6 dB ● Doubling of sound intensity (acoustic energy) belongs to a calculated level change of +3 dB. +10 dB is the level of twice the perceived volume or twice as loud (loudness) in psychoacoustics − mostly sensed. +6 dB is the level of twice the (RMS) value of voltage respectively sound pressure − mostly measured ● +3 dB is the level of twice the energy or power respectively intensity − mostly calculated. For voltage and sound pressure in acoustics the measured RMS value (root mean square) is usually specified. For sinusoidal AC signals, the peak value V0 or p0 is denoted by the term amplitude. VRMS = | V0 | / √ (2). |
| The doubling of the factor (twice the factor) means: for the loudness level: +10 dB, for the sound pressure level: +6 dB SPL and for the electric voltage level: +6 dB, for the sound intensity level: +3 dB and for the power (energy) level: +3 dB ... and 10 dB SPL more means, the amplifier needs 10 times more power. |
| 20 dB gain change should give about the ratio of 4 (four times) for sensed volume and loudness, 20 dB gain change gives the ratio of 10 for measured voltage and sound pressure and 20 dB gain change gives the ratio of 100 for calculated sound power and acoustic intensity. |
| Decibel (dB) can also mean dBSPL or dBA; but a level change is always in decibels dB. The sensed volume or the loudness of a sound depends on several factors: the amplitude, the sound pressure level, the frequency, and the time behaviour of the sound. A typical question on the internet: "Are 3 dBs or 6 dBs double the loudness (or twice as loud)?" Answer: "It's neither 3 dB, nor 6 dB − it's closer to 10 dB more." |
The human perception of loudness
Sound Level Comparison Chart and the Ratio
| Table of sound level dependence and the change of the respective ratios of subjective
volume (loudness), objective sound pressure (voltage), and sound intensity (acoustic power). How many decibels (dB) level change is double, half, or four times as loud? How many dB appear twice as loud (two times)? Here are all the different ratios. Ratio means "how many times" or "how much" ... Doubling of loudness. |
| Level change |
Volume Loudness |
Voltage Sound pressure |
Acoustic Power Sound Intensity |
| +60 dB | 64 | 1000 | 1000000 |
| +50 dB | 32 | 316 | 100000 |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31.6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2.0 = double | 3.16 = √10 | 10 |
| +6 dB | 1.52 times | 2.0 = double | 4.0 |
| +3 dB | 1.23 times | 1.414 times = √2 | 2.0 = double |
| - - - - ±0 dB - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - - - | - - - - 1.0 - - - - - |
| −3 dB | 0.816 times | 0.707 times | 0.5 = half |
| −6 dB | 0.660 times | 0.5 = half | 0.25 |
| −10 dB | 0.5 = half | 0.316 | 0.1 |
| −20 dB | 1/4 = 0.25 | 0.100 | 0.01 |
| −30 dB | 0.125 | 0.0316 | 0.001 |
| −40 dB | 0.0625 | 0.0100 | 0.0001 |
| −50 dB | 0.0312 | 0.0032 | 0.00001 |
| −60 dB | 0.0156 | 0.001 | 0.000001 |
| Log. size | Psycho size | Field size | Energy size |
| dB change | Loudness multipl. | Amplitude multiplier | Power multiplier |
| Ratio / Factor |
Change in Sound Loudness Level |
Change in Sound Pressure Level |
Change in Sound Power Level |
| 40 | +53.22 dB | +32.04 dB | +16.02 dB |
| 30 | +49.07 dB | +29.54 dB | +14.77 dB |
| 20 | +43.22 dB | +26.02 dB | +13.01 dB |
| 15 | +39.07 dB | +23.52 dB | +11.76 dB |
| 10 | +33.22 dB | +20 dB | +10 dB |
| 5 | +23.22 dB | +13.98 dB | +6.99 dB |
| 4 | +20 dB | +12.04 dB | +6.02 dB |
| 3 | +15.58 dB | +9.54 dB | +4.77 dB |
| 2 | +10 dB | +6.02 dB | +3.01 dB |
| - - - - - 1 - - - - - | - - - - ±0 dB - - -- - | - - - - ±0 dB - - - -- | - - - - ±0 dB - - -- - |
| 1/2 = 0.5 | −10 dB | −6.02 dB | −3.01 dB |
| 1/3 = 0.3333 | −15.58 dB | −9.54 dB | −4.77 dB |
| 1/4 = 0.25 | −20 dB | −12.04 dB | −6.02 dB |
| 1/5 = 0.2 | −23.22 dB | −13.98 dB | −6.99 dB |
| 1/10 = 0.1 | −33.22 dB | −20 dB | −10 dB |
| 1/15 = 0.0667 | −39.07 dB | −23.52 dB | −11.76 dB |
| 1/20 = 0.05 | −43.22 dB | −26.02 dB | −13.01 dB |
| 1/30 = 0,033 | −49.07 dB | −29.54 dB | −14.77 dB |
| 1/40 = 0,025 | −53.22 dB | −32.04 dB | −16.02 dB |
| The loudness ratio 4 (four times the loudness) changes the sound loudness level by 20 dB. The sound pressure ratio 4 (four times the pressure) changes the sound pressure level by 12.04 dB. The sound power ratio 4 (four times the intensity) changes the sound power level by 6.02 dB. |
| The loudness ratio 3 (three times the loudness) changes the sound loudness level by 15.58 dB. The sound pressure ratio 3 (three times the pressure) changes the sound pressure level by 9.54 dB. The sound power ratio 3 (three times the intensity) changes the sound power level by 4.77 dB. |
| The loudness ratio 2 (two times (twice) the loudness) changes the sound loudness level by 10 dB. The sound pressure ratio 2 (two times the pressure) changes the sound pressure level by 6.02 dB. The sound power ratio 2 (two times the intensity) changes the sound power level by 3.01 dB. |
| Loudness is a subjective feeling that is often confused with objective SPL measurements in decibels. With sound level we usually mean a logarithmic ratio of measurable sound pressures. The number of sones to a phon was chosen so that a doubling of the number of sones sounds to the human ear like a doubling of the loudness, which also corresponds to increasing the sound pressure level by (+)10 dB, or increasing the sound pressure by a ratio 3.16 = root of 10. "What are sones and phons?": http://www.sengpielaudio.com/calculatorSonephon.htm |
Sound loudness - Sound pressure - Sound intensity
The factors and their levels in decibels (dB).
Loudness perception - sound pressure effect - sound intensity cause
|
|
Sound loudness - Sound pressure - Sound intensity
Different wines. The wine in the middle tastes best.
"Loudness" should never be mixed or set equal to "intensity".
|
| Realm of Psychoacoustic - Relationship between phon and sone
Conversion of sound units (levels) Total Level Calculation (Adding of levels) Factor or Ratio and Level in Decibels (dB) |
The often unknown formulas for level and ratio.
Loudness formula - pressure formula - intensity formula
| Psychoacoustics − Level change loudness 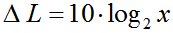 |
Ratio for "loudness" |
| ● Field quantity − Level change sound pressure 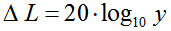 |
● Ratio for "sound pressure" |
| Energy or power quantity − Level change sound intensity 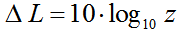 |
Ratio for "sound intensity" |
log to the base 10 = log10 is named lg and log to the base 2 = log2 is named ld.
Δ L = (10/log10(2))·log(x) = 33.22·log (x) = 10·log2(x) x = 10(ΔL/33.22) = 2(ΔL/10)
| A typical question: How many decibels more is the 3-fold subjective loudness? Some people have problems with the idea of "twice as loud", or "three times as loud." I confess − I am one of them. The solution of the top calculator shows 15.85 dB. Hmmm ... The psychoacoustic values of volume (loudness) are always signal, pulse and frequency-dependent. Therefore a statement about this perceived quantity must be viewed with a certain caution. |
|  |
Car freaks und "dB Drag Racing" fans need for their loudspeakers:
![]() The Big Power Formulas
The Big Power Formulas
Electrical and mechanical power calculation
![]()
The psycho-acoustic volume or loudness
is a subjective sensation of size.
| Is 10 dB or 6 dB sound level change for a doubling or halving of the loudness (volume) correct? About the connection between sound level and loudness, there are various theories. Widely accepted is still the theory of psycho-acoustic pioneer Stanley Smith Stevens, indicating that the doubling or halving of the sensation of loudness corresponds to a level difference of 10 dB. Recent research by Richard M. Warren, on the other hand leads to a level difference of only 6 dB. *) This means that a double sound pressure corresponds to a double loudness. The psychologist John G. Neuhoff found that our hearing is more sensitive to rising levels of sound as to falling levels. That is for the same sound level difference the change of loudness from quiet to loud is stronger than from loud to quiet. It is suggested that the sone scale of loudness reflects the influence of known experimental biases and hence does not represent a fundamental relation between stimulus and sensation. *) Richard M. Warren, "Elimination of Biases in Loudness Judgments for Tones", 1970, Journal of the Acoust. Soc. Am. Volume 48, Issue 6B, pp. 1397 - 1403 and Richard M. Warren, "Quantification of Loudness", 1973, American Journal of Psychology, Vol 86 (4), pp. 807 - 825 John G. Neuhoff, "An adaptive bias in the perception of looming auditory motion", 2001, Ecological Psychology 13 (2) pp. 87 - 110 and John G. Neuhoff, "Perceptual Bias for Rising Tones", 1998, Nature, Volume 395, 10 September Citation: When known experimental biases were eliminated, half loudness was equal to half sound pressure level (−6 dB) from 45 to 90 dB. It follows that the determination of the volume (loudness) which is double as loud should not be dogmatically defined. More realistic is the following claim: |
| A doubling of the sensed volume (loudness) is equivalent to a level change approximately between 6 dB and 10 dB. |
| ... by the way: You cannot usefully double or multiply any "level". There is double voltage and double sound pressure. What is double the level? 3 dB, 6 dB or 10 dB? Aha - therefore it's better to avoid this expression. "Double the level" means carelessly, that there is really double the voltage. The expression: "Double the level equals 3 dB" is nonsense. What is the doubling of 10 decibel? That is no good question. |
| Typical question: Is 3 decibel more level twice as loud? Answer: No! Psychoacousticians tell us, that we must feel a level boost of 6 to 10 dB as twice as loud. |
Level dynamics and spectral dynamics (timbre dynamics)
| Equally important as the level dynamics, is the timbre dynamics, also called spectral dynamics. The perceived volume (loudness) is almost independently characterized by amplitude level through a specific timbre spectrum range played by musical instruments as dynamic stages. |
| A weighting filter is used to emphasise or suppress some aspects of a phenomenon compared to others for measurement or other purposes. In the measurement of loudness, for example, an A-weighting filter is commonly used to emphasize frequencies around 3 to 6 kHz where the human ear is most sensitive, while attenuating very high and very low frequencies to which the ear is insensitive. The aim is to ensure that measured loudness corresponds well with subjectively perceived loudness. A-weighting is only really valid for relatively quiet sounds and for pure tones as it is based on the 40-phon equal-loudness contour; see the weighting filtered levels dBA and dBC. |
| Another difficult issue is: How does the volume (loudness) decrease with distance from a sound source? How does the sound pressure (voltage) decrease with distance from a sound source? How does the sound intensity (not the sound power) decrease with distance from a sound source? The beginners question is quite simple: How does the sound decrease with distance? |
![]()
Adding of equal strong non-coherent sound sources
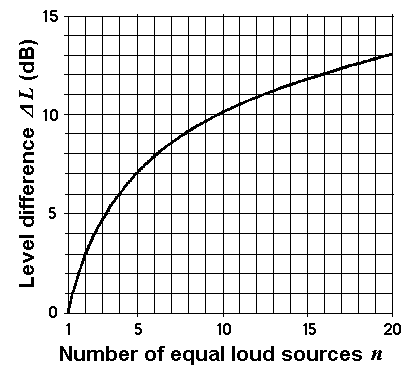 |
|
||||||||||||||||||||||||||||||
Formulas: Δ L = 10×log n or n = 10(ΔL/10)
Δ L = level difference; n = number of equal loud sound sources.
| n = 2 equally loud incoherent sound sources result in a higher level of 10 × log 2 = +3.01 dB compared to the case that only one source is available. n = 3 equally loud incoherent sound sources result in a higher level of 10 × log 3 = +4.77 dB compared to the case that only one source is available. n = 4 equally loud incoherent sound sources result in a higher level of 10 × log 4 = +6.02 dB compared to the case that only one source is available. |
Calculator: Adding level of equal loud sound sources
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
The total level in decibels is the level of one sound source plus the increase of level in dB.
| The very special case of active noise cancellation (compensation) by obliterating level addition - which is labeled "Active noise control" - is not considered here. |
The decrease of sound with distance
| For a spherical wave we get: The sound pressure level (SPL) decreases with doubling of distance by (−)6 dB. The sound pressure falls to 50% or 1/2 fold of the initial value of the sound pressure. The sound pressure decreases with the ratio 1/r of the distance. The sound intensity level decreases with doubling of distance also by (−)6 dB. The intensity falls to 25% or 1/4 fold of the initial value of the acoustic or sound intensity. The sound intensity decreases with the ratio 1/r2 of the distance. The loudness level decreases with doubling of distance also by (−)6 dB. The loudness falls to 63% or ca. 2/3 fold of the initial value of the sensed loudness. The loudness decreases with the ratio 1/(20.66 r) = 1/1.581 r to the distance. Levels of sound pressure and levels of sound intensity decrease equally with the distance from the sound source. Sound power or sound power level has nothing (!) to do with the distance from the sound source. Thinking helps:A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time. Watts don't change with distance. |
Sound pressure and Sound power − Effect and Cause
| The doubling of the "loudness impression" will require an increase of sound pressure level
of about 10 dB. Who knows exactly how loud the sensation "sounds twice as loud" is?
A measurement of the doubling of the sound pressure, however, equals exactly +6 dB. |
Frequently used false statements in the context of
sound values and the distance of the sound source
| Correct version | Wrong expression |
| Sound pressure (amplitude) falls inversely proportional to the distance 1/r from the sound source. That is the 1/r law or the inverse distance law. |
Sound pressure (amplitude) falls inversely proportional to the square of the distance 1/r2 from the sound source. really wrong |
| Sound pressure level decreases by (−)6 dB for doubling of the distance from the source to 1/2 (50 %) of the sound pressure initial value. |
Sound pressure level decreases as the distance increases for doubling of the distance from the source by (−)3 dB. wrong |
| Sound intensity (energy) falls inversely proportional to the square of the distance 1/r2 from the sound source. That is the inverse square law 1/r2. |
Sound intensity (energy) falls inversely proportional to the distance 1/r from the sound source. wrong |
| Sound intensity level decreases by (−)6 dB for doubling of the distance from the source to 1/4 (25 %) of the sound intensity initial value. |
Sound intensity level decreases inversely as the square of the distance increases for doubling of the sound source by (−)3 dB. wrong |
Sound pressure is not intensity
| Neither the sound power nor the sound power level decreases in doubling the distance. Why is this so? The sound power level quantifies the totally radiated sound energy from an object. Different to the sound pressure the sound power is independent of the distance to the sound source, the surrounding area and other influences. |
| How does the sound decrease with distance? |
| Knowing the intensity of a sound wave allows one to calculate the decibel (dB) level of that sound. Use the Decibel Calculator widget to determine the decibel rating from any intensity in watt/meter2. Enter intensities using scientific notation − for example, enter 5e^−5 for 5.0×10−5. |
| WolframAlpha Decibel Calculator |
| Determine the perceived loudness of a sound |
| Half loudness ≡ level –10 dB | Double loudness ≡ level +10 dB |
| Half sound pressure ≡ level –6 dB | Double sound pressure ≡ level +6 dB |
| Half power ≡ level –3 dB | Double power ≡ level +3 dB |
| Four times power ≡ level +6 dB | Ten times power ≡ level +10 dB |
| Double distance ≡ level –6 dB | Double sources (Double power) ≡ +3 dB |
| Simple rule of thumb: When working with power, 3 dB means double (twice) the factor and 10 dB means 10-fold. When working with voltage or current, 6 dB means double (twice) the factor and 20 dB means 10-fold. |
| back |
Search Engine |
home |