Combining and adding decibels of one-third octave bands to level of octave bands adding dB EQ 1/3 octave band finding number 1/3 octaves between frequencies analysys filter 1/1 octave band filter oct calculator calculation 1/3 octave band to octave band conversion iso frequency bands EQ equalizer

Adding decibels of one-third octave bands
to level of one octave band and vice versa

● Spectral data analysis − spectrum analyzer − one-third octave band = 1/3 octave band ●
Filter Equalizer EQ

The used browser does not support JavaScript.
You will see the program but the function will not work.

Three adjacent one-third octave bands (1/3 octave bands) belong to one octave band.

Should the level of an octave band be converted to one-third octave
bands, the energy of the octave band can be divided by three. This
corresponds to a reduction of (−)4.771 dB for each 1/3 octave band.

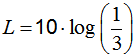
one-third octave

Calculate: Octave band level L_Σ of three one-third octave band levels L₁, L₂, and L₃:

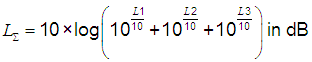
Sum Level

Calculator: Adding of equal levels of 1/3 octave bands

Octave-band filters (1/1) and one-third octave-band filters (1/3)

Simply enter the value to the left or the right side.
The calculator works in both directions of the ↔ sign.

The total level in dB is the level of one band plus the increase in level.

Octave bands One-third octave bands

ISO Band numbers	Octave band Center frequency	One-third octave band Center frequencies
11, 12, 13	16 Hz	12.5 Hz, 16 Hz, 20 Hz
14, 15, 16	31.5 Hz	25 Hz, 31.5 Hz, 40 Hz
17, 18, 19	63 Hz	50 Hz, 63 Hz, 80 Hz
20, 21, 22	125 Hz	100 Hz, 125 Hz, 160 Hz
23, 24, 25	250 Hz	200 Hz, 250 Hz, 315 Hz
26, 27, 28	500 Hz	400 Hz, 500 Hz, 630 Hz
29, 30, 31	1000 Hz	800 Hz, 1000 Hz, 1250 Hz
32, 33, 34	2000 Hz	1600 Hz, 2000 Hz, 2500 Hz
35, 36, 37	4000 Hz	3150 Hz, 4000 Hz, 5000 Hz
38, 39, 40	8000 Hz	6300 Hz, 8000 Hz, 10000 Hz
41, 42, 43	16000 Hz	12500 Hz, 16000 Hz, 20000 Hz

Standard frequencies for acoustic measurements according to EN ISO 266

1st octave cycle	31.5						63						125						250
2nd octave cycle				45						90						180
1st 1/3 octave cycle	31.5		40		50		63		80		100		125		160		200		250
2nd 1/3 octave cycle		35,5		45		56		71		90		112		140		180		224		280
1st octave cycle					500						1000						2000
2nd octave cycle		355						710						1400						2800
1st 1/3 octave cycle	315		400		500		630		800		1000		1250		1600		2000		2500
2nd 1/3 octave cycle		355		450		560		710		900		1120		1400		1800		2240		2800
1st octave cycle			4000						8000						16000
2nd octave cycle						5600						11200						22400
1st 1/3 octave cycle	3150		4000		5000		6300		8000		10000		12500		16000		20000		25000
2nd 1/3 octave cycle		3550		4500		5600		7100		9000		11200		14000		18000

Center, lower, and upper frequencies for standard set of octave
and 1/3 octave bands covering the audible frequency range.

Octave Band			1/3 Octave Band
Lower Frequency f₁ (Hz)	Center Frequency f₀ (Hz)	Upper Frequency f₂ (Hz)	Lower Frequency f₁ (Hz)	Center Frequency f₀ (Hz)	Upper Frequency f₂ (Hz)
22	31.5	44	22.4	25	28.2
			28.2	31.5	35.5
			35.5	40	44.7
44	63	88	44.7	50	56.2
			56.2	63	70.8
			70.8	80	89.1
88	125	177	89.1	100	112
			112	125	141
			141	160	178
177	250	355	178	200	224
			224	250	282
			282	315	355
355	500	710	355	400	447
			447	500	562
			562	630	708
710	1,000	1,420	708	800	891
			891	1,000	1,122
			1,122	1,250	1,413
1,420	2,000	2,840	1,413	1,600	1,778
			1,778	2,000	2,239
			2,239	2,500	2,818
2,840	4,000	5,680	2,818	3,150	3,548
			3,548	4,000	4,467
			4,467	5,000	5,623
5,680	8,000	11,360	5,623	6,300	7,079
			7,079	8,000	8,913
			8,913	10,000	11,220
11,360	16,000	22,720	11,220	12,500	14,130
			14,130	16,000	17,780
			17,780	20,000	22,390

A, B, and C Electrical Weighting Networks for the Sound-Level Meter. These numbers assume a diffuse-field (random incidence) response for the sound level meter and microphone.

Frequency (Hz)	A-weighting relative response (dB)	B-weighting relative response (dB)	C-weighting relative response (dB)
25 31.5 40	−44.7 −39.4 −34.6	−20.4 −17.1 −14.2	−4.4 −3.0 −2.0
50 63 80	−30.2 −26.2 −22.5	−11.6 −9.3 −7.4	−1.3 −0.8 −0.5
100 125 160	−19.1 −16.1 −13.4	−5.6 −4.2 −3.0	−0.3 −0.2 −0.1
200 250 315	−10.9 −8.6 −6.6	−2.0 −1.3 −0.8	0 0 0
400 500 630	−4.8 −3.2 −1.9	−0.5 −0.3 −0.1	0 0 0
800 1,000 1,250	−0.8 0 +0.6	0 0 0	0 0 0
1,600 2,000 2,500	+1.0 +1.2 +1.3	0 −0.1 −0.2	−0.1 −0.2 −0.3
3,150 4,000 5,000	+1.2 +1.0 +0.5	−0.4 −0.7 −1.2	−0.5 −0.8 −1.3
6,300 8,000 10,000	−0.1 −1.1 −2.5	−1.9 −2.9 −4.3	−2.0 −3.0 −4.4
12,500 16,000 20,000	−4.3 −6.6 −9.3	−6.1 −8.4 −11.1	−6.2 −8.5 −11.2

The total level adding of incoherent sound sources means power sum and power addition or sound power sum and sound power addition

Adding decibels - combining up to (10) ten acoustic levels
Adding decibels - combining up to (30) thirty acoustic levels
Calculate the center frequency of a frequency band - geometric mean
Calculate: Q Factor and center frequency - Find the −3 dB cutoff frequencies
Total level adding of incoherent sound sources
Sound measuring (Noise measuring) - Conversion: Frequency f to dBA and dBC

Generation law for octave and third octave bands

Octave band − oct. filter		1/3 Octave band − third oct. filter

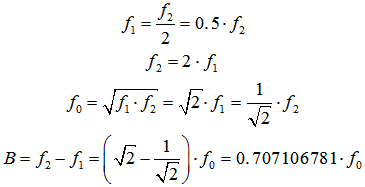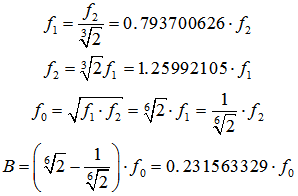f₁ = Lower cut-off frequency of the octave or 1/3 octave in Hz f₂ = Upper cut-off frequency of the octave or 1/3 octave in Hz f₀ = Center frequency of the octave or 1/3 octave in Hz B = Bandwidth (BW) of the filter f₂ − f₁ in Hz

[top of page]

back

Search Engine

home


Number of 1/3 oct bands n	↔	Increase of level *Δ L* dB

Three 1/3 octave bands are one octave band