Total dB level adding of incoherent or noncoherent uncorrelated sound sources signals combine sound levels two sources resultant level audio logarithmic decibel scale decibels or SPL sound pressure level add signal noise levels noncoherent incoherent random phase acoustic

Sound calculations
● Total level adding of incoherent sound sources ●
Fact: Power sum and Power addition or
Sound power sum and Sound power addition

Adding the level of two uncorrelated signals,
Combining acoustical levels of e.g. a violin and a violoncello
as power sum (total power).
For beginners: incoherent or noncoherent (random phase) means that the signals of the channels are irrelative like a violin
and a cello having no correlative relationship. Often we say contantly changing or uncorrelated when we mean incoherent.

The used browser does not support JavaScript.
You will see the program but the function will not work.

Decibels are logarithmic "units", they may not be added linearly like other figures.
In most cases we will add uncorrelated signals as noise or music. If a sound source creates a sound level (SPL) of L₁ = 60 dB and another source with L₂ = 60 dB is added, then it is not the level of 120 dB, but gives an incoherent (noncoherent) summing of the signal level of 63 dB. If both values are equal, it is easy.
More than 3 dB greater than the higher of the two incoherent levels is not possible for the total sum in decibels.
See also the other case:
● Total level adding of electrical coherent signals.

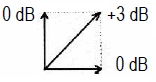
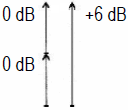
Adding amplitudes (and levels)


Power sum incoherent (90°) √ (1² + 1²) = 1,414...		Voltage sum coherent (0°) 1 + 1 = 2

Adding of two incoherent (noncoherent) sound pressure levels or voltage levels:

Adding of two values of the same level results an increase of the total level of (+)3 dB.
This equation is used for electrical adding of incoherent signals, and for the calculation of the energy level of two loudspeakers.

Adding of two coherent sound pressure levels or voltage levels:

Adding of two values of the same level results an increase of the total level of (+)6 dB.
This is obtained by feeding two side-by-side loudspeakers with the same signal.

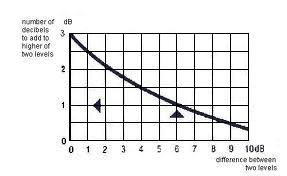
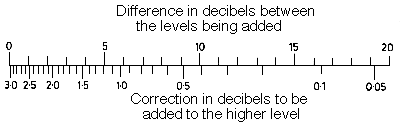Combined Sound Pressure Levels - sengpielaudio

Level difference between the two sound sources

Adding of two different acoustical levels

For the sound level of n incoherent radiating sound sources we get: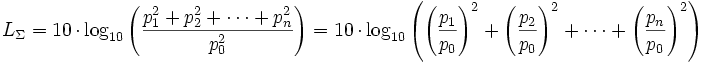
SPL Addition 01

p₀ is the reference value of the sound pressure. Auditory threshold at 1 kHz = 0.00002 Pa = 20 µPa.

Level adding of up to four sound sources

Adding Amplitudes and Levels - incoherent and coherent
Adding decibels - combining up to ten acoustic levels
Combining decibels of one-third octave bands to level of octave band and vice versa
How many decibels (dB) sound level change is twice (double, half) or three times as loud?
Damping of sound level with distance
How does the sound decrease with distance?
How do Sound Pressure Levels add when listening?
What is Amplitude? Amplitude of a sound - particle displacement and sound pressure

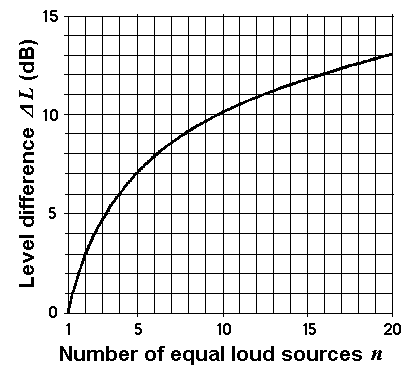
Adding of equal loud incoherent sound sources

Level increase Δ L for n equal loud sound sources
Number of n equal loud sound sources	Level increase Δ L in dB
1	0
2	3.0
3	4.8
4	6.0
5	7.0
6	7.8
7	8.5
8	9.0
9	9.5
10	10.0
12	10.8
16	12.0
20	13.0

Formulas: Δ L = 10 × log n or n = 10^(ΔL/10)
Δ L = level difference; n = number of equal loud sound sources.

n = 2 equally loud incoherent sound sources result in a higher level of
10 × log₁₀ 2 = +3.01 dB compared to the case that only one source is available.
n = 3 equally loud incoherent sound sources result in a higher level of
10 × log₁₀ 3 = +4.77 dB compared to the case that only one source is available.
n = 4 equally loud incoherent sound sources result in a higher level of
10 × log₁₀ 4 = +6.02 dB compared to the case that only one source is available.
n =10 equally loud incoherent sound sources result in a higher level of
10 × log₁₀ 10 = +10.00 dB compared to the case that only one source is available.

Adding (combining) levels of equal loud sound sources

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

The total level in dB is the level of one sound source plus the increase of level in dB.

What does sound level mean?

A reduction of the sound power level of the sound source by 6 dB is resulting in a reduction of the sound pressure level and the sound intensity level at the location of the receiver by also 6 dB, even if the sound power drops to a factor of 0.25, the sound pressure drops to a factor of 0.5 and the sound intensity drops to a factor of 0.25. The reference value for the sound level was chosen so that with a characteristic acoustic impedance of Z₀ = ρ · c = 400 N·s/m³ the sound intensity level results in the same value as the sound pressure level. We therefore simply speak of the "sound level" and leave it open whether sound pressure level or sound intensity level is meant.

Sound engineers and sound protectors ("ear people") think by the short word
"sound level" simply of "sound pressure level" (SPL) as sound field quantity.
Acousticians and sound protectors ("noise fighters") mean by the short word
"sound level" probably "sound intensity level" as sound energy quantity.
Equating sound pressure with sound intensity must cause problems. I ~ p².

back

Search Engine

home

Equal strong incoherent (non-coherent) sound sources
Number of sound sources n	↔	Increase of level ΔL dB