

| Deutsche Version |
 |
| Because the speed of sound c increases by 0.6 m/s per degree Celsius,
the pitch of wind instruments - that means the frequency - also rises by
about three cents (3/100 of a semitone). The effect on the pitch change of an instrument (brass and woodwind) from the expansion of its material is insignificant. |
Change of pitch J (frequency) depending on the ambient temperature ϑ (theta)
of vibrating air columns, such as flutes, whistles and other wind instruments
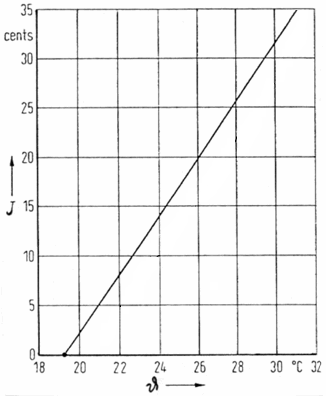 |
From: U. Pisani, "Effect of a Local Temperature Change in an Organ Pipe", Acustica, Vol.25 (1976), pp.133 ff.
| You need to understand that for a note (tone) of a pipe organ or of another wind instrument − when the temperature increases from 20°C to 25°C − the speed of sound c and thus the product of λ × f will be changed. Since the length of the organ pipe and with it the wavelength λ remain constant, only the frequency f (pitch) will change. |
| c = λ × f |
λ = c / f | f = c / λ | c ~ f |
| The influence of temperature is independent of pitch, therefore always the same. This means that the determined deviation in cents is true for each note. The value in cents is independent of frequency. |
| Conversion of frequency ratio y = f2 / f1 to interval ratio J in cents: J in cents = 1200 × (log y / log 2) Conversion of interval ratio J in cents to frequency ratio y: y = f2 / f1 = 10J×log (2/1200) |
| The following formula gives the exact speed of sound, as it changes with temperature: Speed of sound 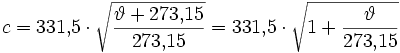 in m/s in m/sTemperature ϑ in °C |
| Frequency ratio (frequency change) change with temperature |
|
| The influence of temperature on pitch: The speed of sound in air and thus the pitch (frequency) of
a note as a column of air of a certain length is directly proportional to the square root of its
absolute temperature. The absolute temperature is measured from Absolute Zero, which is minus
273.15°C. The unit is the degree Kelvin (K); 1 K has the same size as 1°C. Example: The frequency change from an increase in temperature of ϑ1 = 20°C to ϑ2 = 24°C is the square root of [(273 + 24 = 297 K) / (273 + 20 = 293 K)] = 1.0069028 ... Therefore an increased frequency of 440 Hz at 20 C (440 Hz × 1.0069028) = 443 Hz at 24° C. It should be noted that the temperature of the air inside the wind instrument is rather complex. It lies between the temperature of the room and that of the body of the player. The instrument heats up and the pitch of the note rises. |
| A trained listener notices a deviation from the true pitch at about 5 cents. A person with normal hearing needs 10 cents for recognition. This refers to notes played in succession. Two notes differing by 5 cents played simultaneously will produce quite strong audible beating. |
|
Change of pitch with change of temperature: Conversion of frequencies and intervals to cents Temperature Dependence of Physical Quantities Sound pressure and Sound power − Effect of temperature Change of pitch with change of level: Effect of Loudness Changes on Perceived Pitch: S. S. Stevens, "The attributes of tones (1934) PNAS 1934 20 (7) 457 - 459" At low frequencies the pitch of sinus tones seem to increase slightly as loudness decreases - or: At high frequencies the pitch of sinus tones seem to increase slightly as loudness increases. The effect is clearly audible only to pure (sinusoidal) tones. Complex tones show no perceived pitch changes with level changes. With resounding tongues (accordion), the oscillation is independent of the medium (air, water, even in vacuum) and the temperature. The tongue vibrates always exactly in the same way. |
Frequency to Wavelength and reverse
| Simply enter the value to the left or the right side. The calculator works in both directions of the ↔ sign. |
Speed of Sound and Temperature in Air
| Simply enter the value to the left or the right side. The calculator works in both directions of the ↔ sign. |
Fahrenheit to Celsius and Celsius to Fahrenheit
| Simply enter the value to the left or the right side. The calculator works in both directions of the ↔ sign. |
| For a one-degree increase in temperature the speed of sound increases
by 0.6 meters per second. Expressed in percentage that is 0.6 / 343.5 = 0.00175 = 0.175%. A semitone is a 5.95% change in frequency. Since 0.175 / 5.95 = 0.03, we expect a pitch change of about 3 cents for each one-degree Celsius change in temperature with woodwinds. Remember, a "cent" in this context is one hundredth of a semitone, just as a semitone is one twelfth of an octave. |
| Some persons have the ability to identify absolutely the pitch of a musical note without the help of first hearing a reference note. Scientists generally call the phenomenon "absolute pitch", while musicians tend to refer to it as "perfect pitch". The terms are used interchangeably. |
A typical question: What is the relationship between wavelength, temperature and frequency?
| back |
Search Engine |
home |