cents to frequency ratios conversion and convert frequency ratio to cent interval Hz cps pitch piano tuning calculator audio change fraction TET cents to hertz (herz) calculator ¢ minor third major semitone convert hertz to semitones equation semi tone keyboard

$cents to frequency ratios conversion convert frequency ratio to cent interval Hz piano tuning calculator pitch audio change fraction TET cents to hertz (herz) ¢ minor third major calculator ¢ convert hertz to semitones equation keyboard - sengpielaudio$

Deutsche Version

● Conversion of Intervals − ¢ = cent ●

• Frequency ratio to cents and cents to frequency ratio •

Change of pitch with change of temperature

1 hertz = 1 Hz = cps = cycles per second
The unit most commonly used to measure intervals is called cent, from Latin centum,
meaning "one hundred". It stands for one hundredth of an equal-tempered semitone.
In other words, one octave consists of 1200 cents.

The used browser does not support JavaScript.
You will see the program but the function will not work.

Fill out the gray boxes and click at the calculation bar.

How many cents are in a hertz?
There is no conversion from Hz to cents and vice versa.
Scroll down to the bottom: "Table of Cent Difference".
Statement: Cent is a logarithmic unit of measure of an interval, and that is a dimensionless "frequency ratio" of f₂ / f₁.

Calculation: Intervals (cents) and Frequency (Hz) as Excel Program (xls)

Different Thirds
Thirds

Cent value-determination of an interval

Instead of the frequencies you can take the fraction numbers − e.g. 4/5 of the interval major third.

Formula for converting the interval frequency ratio f₂ / f₁ to cents (c or ¢).

¢ or c = 1200 × log₂ (f₂ / f₁)
log 2 = 0.301029995

This formula employs a log 2, or logarithm base 2 function. This formula can also be
written using a log 10 function, available on most scientific calculators via the log button:

c = 1200 × 3.322038403 log₁₀ (f₂ / f₁)
1/log 2 = 1/0.301029995 = 3.322038403

The formula expressed using log₁₀ rather than log 2.

3.322038403 is a conversion factor that converts base 2 logarithms to base 10 logarithms.
1 Cent = 2^(1/1200) = 1.0005777895065548592967925757932
One cent is thus the number that multiplied by itself 1200 times results in the number 2.
The cent is an interval which is calculated from the interval frequency ratio as follows:
(In of the interval frequency ratio / ln 2)×1200 = cents value of the interval.
An interval of a halftone is equivalent to: 2(1/12) = 1,0594630943592952645618252949463.
That is: [ln (2(1/12)) / ln (2)]×1200 cent = 100 cent.

The Pythagorean comma is the frequency ratio (3 / 2)¹² / 2⁷ =
3¹² / 2¹⁹ = 531441 / 524288 = 1.0136432647705078125.
The resulting is converted to 23.460010384649013 cent.
Twelve perfect fifths (3 / 2) reveals 8423.46 cents and
seven octaves, however, reveals only 8400 cents.

Conversions of Semitone Intervals
An interval is the difference between two pitches or the
distance between two frequencies in terms of semitones.

Enter any two known values and press "calculate" to solve for the other. Please, enter only two values.

Frequency calculation for different octave intervals

Change of pitch with change of temperature

Changing of the frequency about a cent value

Frequency to musical note converter

Find out what note a given frequency is. English system.

Formulas: f = 440 × 2^(−58/12) × (2^(1/12))ⁿ and f = 440 × 2^{((n−58)/12)}

The original source program of Iain W. Bird is still faulty:
http://www.birdsoft.demon.co.uk/music/notecalc.htm

The frequency of 440 Hz is the concert pitch note A4.
If someone tells you different, this person is in error; see also:

Table: Frequencies of equal temperament and Note names

Change of pitch with change of temperature

The frequency as semitone distance from A4 = 440 Hz

For a note that lies n semitones higher (or −n semitones lower) from A4, the frequency is f_n = 2^n/12 × 440 Hz.
Conversely, one can obtain n, the number of semitones from A4, from:
n = 12 × log₂(f_n / 440 Hz).

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Masterclock calculator (clock rate)

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Calculator with reference frequency

For downward tuning the reference frequency and piano tuning can be changed.

100 cent is equivalent to a semitone (halftone).

Note names: English and German System by comparison

Calculations of Harmonics from Fundamental Frequency

Change of pitch with change of temperature

Octave division in 12-tone equal temperament TET

Interval	Frequency ratio	cents
Unison	1.000000 : 1	0
Semitone or minor second	1.059463 : 1	100
Whole tone or major second	1.122462 : 1	200
Minor third	1.189207 : 1	300
Major third	1.259921 : 1	400
Perfect fourth	1.334840 : 1	500
Augmented fourth/Diminished fifth	1.414214 : 1	600
Perfect fifth	1.498307 : 1	700
Minor sixth	1.587401 : 1	800
Major sixth	1.681793 : 1	900
Minor seventh	1.781797 : 1	1000
Major seventh	1.887749 : 1	1100
Octave	2.000000 : 1	1200

Some like to tell us that calling a tempered fifth "perfect"
is a misnomer and perfect intervals are only proper fractions.

Keyboard

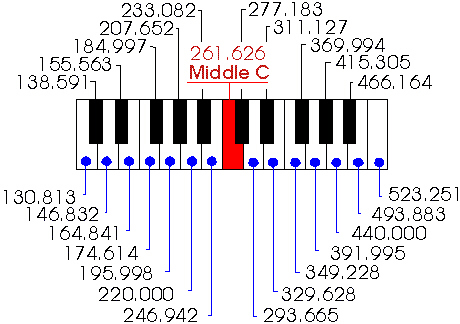
In the following table are for the most popular pure dyads up to the octave - the frequency ratio is themeasure of consonance and the sound sensation of most people.

Dyads	Frequency ratio	Consonance value	Sensation of sound
minor second	16:15	15.49	very dissonant
major second	9:8	8.49	dissonant
minor third	6:5	5.48	consonant ("minor")
major third	5:4	4.47	consonant ("major")
forth	4:3	3.46	consonant
tritonus	45:32	37.95	very dissonant
fifth	3:2	2.45	very consonant ("neutral")
minor sixth	8:5	6.32	consonant ("minor")
major sixth	5:3	3.87	consonant ("major")
minor seventh	16:9	12.00	dissonant
major seventh	15:8	10.95	dissonant
octave	2:1	1.41	very consonant ("neutral")

Name	Exact value in 12-TET	Decimal value	Just intonation interval	Percent difference
Unison	1	1.000000	1 = 1.000000	0.00%
Minor second		1.059463	16/15 = 1.066667	−0.68%
Major second		1.122462	9/8 = 1.125000	−0.23%
Minor third		1.189207	6/5 = 1.200000	−0.91%
Major third		1.259921	5/4 = 1.250000	+0.79%
Perfect fourth		1.334840	4/3 = 1.333333	+0.11%
Diminished fifth		1.414214	7/5 = 1.400000	+1.02%
Perfect fifth		1.498307	3/2 = 1.500000	−0.11%
Minor sixth		1.587401	8/5 = 1.600000	−0.79%
Major sixth		1.681793	5/3 = 1.666667	+0.90%
Minor seventh		1.781797	16/9 = 1.777778	+0.23%
Major seventh		1.887749	15/8 = 1.875000	+0.68%
Octave		2.000000	2/1 = 2.000000	0.00%

TET 12 - equal temperament semitone (1/2 tone) has the frequency ratio of ¹²√2 = 2^1/12 = 1.0594630943592952645618252949463
TET 24 - equal temperament quarter tone (1/4 tone) has the frequency ratio of ²⁴√2 = 2^1/24 = 1.0293022366434920287823718007739
TET 48 - equal temperament eighth tone (1/8 tone) has the frequency ratio of ⁴⁸√2 = 2^1/48= 1.0145453349375236414538678576629

Question: How can I convert cents to Hz?
Answer: You cannot convert cents to hertz, because cents are not a frequency.
cents are the measurement between intervals, that is a "frequency ratio" f₂/f₁.

Here's a Table of Cents Difference for some frequencies close around 440 Hz:

Frequency	Difference
435 Hz	−19.78 cents
436 Hz	−15.81 cents
437 Hz	−11.84 cents
438 Hz	−7.89 cents
439 Hz	−3.94 cents
440 Hz	±0 cent
441 Hz	+3.93 cents
442 Hz	+7.85 cents
443 Hz	+11.76 cents
444 Hz	+15.67 cents
445 Hz	+19.56 cents

So, the conversion factor 4 cents / Hz is valid for the purposes of tuning as an exception only very close around 440 Hz.
There is no conversion from Hz to cents and vice versa.
Statement: Cent is a logarithmic unit of measure of an interval, and that is a dimensionless "frequency ratio" of f₂ / f₁.

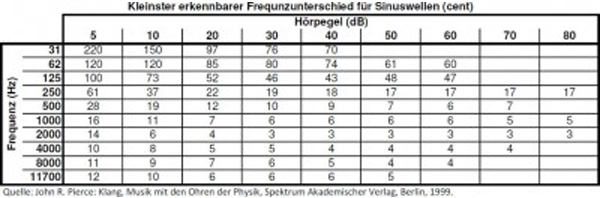
Smallest recognizable frequency difference for pure tones at different listening levels

back

Search Engine

home


Semitone n as distance from A4 Semitones	↔	Frequency f_n - Reference: 440 Hz Hz

*n = 12(log (f_n/440) / log(2)) f_n = 2^(n/12)440*


Reference wordclock 48.0 kHz Piano tuning f Hz	↔	Reference frequency 440 Hz Studio wordclock f_s kHz


Reference wordclock 44.1 kHz Piano tuning f Hz	↔	Reference frequency 440 Hz Studio wordclock f_s kHz