

| Deutsche Version |
|
| Z2 (Zout) is the small internal resistance (source impedance or output impedance) of the first unit
and Z1 (Zin) is the larger external resistance (load impedance, input impedance) of the following
equipment. With resistance R it is always meant the impedance Z. In recording studio technique
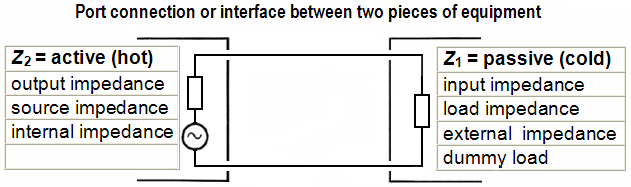
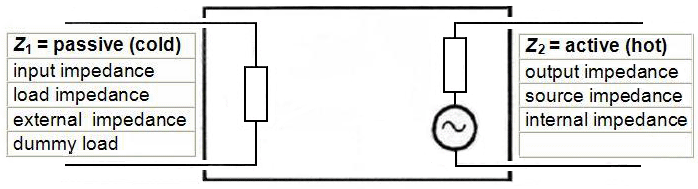
the voltage bridging Z2 < Z1 is used for the interconnection in general, which is a voltage divider. This are great advantages, because it is best for the large frequency bandwidth to be transmitted and by changing loads, by different cable lengths, and by parallel connection of several devices. It keeps the voltage high at the input of the following gear. The impedance matching concept Z2 = Z1 is expected to remain in telecommunications, digital technique, but not in analogue audio. |
|
E-guitars and microphones are sources. They can show us only their output impedance. Amplifier inputs and loudspeakers are loads. They can show us only their input impedance. |
 |
| In recording studio technique the microphone Zsource (Z2) is less than 200 ohms and Zload (Z1) of the mixer (pre-amp) is between 1000 and 2000 ohms. A voltage loss by attenuation of less than 1 dB is acceptable in professional audio engineering. The cable resistance (impedance) is a part of the output impedance of the amplifier. Because Voltage at the input of the amplifier = open-circuit voltage of the source × Zload/(Zload+Zsource) |
|
There is no impedance matching Zout = Zin between power amplifier and loudspeakers. Power matching is a myth. We use voltage bridging Zout << Zin. The same goes for tube amplifiers whose output impedance is about one tenth of the speaker impedance. Thus we also have Zout < Zin. That's a fact! Please read this: "8 Ohm Output" and "150 Ohm Input" - What is that? |
| The seldom specified source resistance Z2 (Zout) is hidden in the damping factor DF. A damping factor of at least DF = 100 is entirely in order. Analog studio devices have a source impedance Z2 of less than 40 ohms, with a load impedance of Z1 greater than 10 kiloohms. Zsource << Zload. Impedance matching (power matching) Z1 = Z2 on the other hand, is used in the telecommunications and the RF technology applied to antennas - but not in audio. |
| Notice: There are really no 4 ohm amplifiers and there are no 8 ohm amplifiers for the 4 ohm or 8 ohm loudspeakers. |
| In sound engineering there is no Power matching or Impedance matching. In audio we use only Voltage bridging or high Impedance bridging. |
|
In audio engineering, we use even in power amplifiers which operate the speakers, really only voltage bridging. The frequent demand for "real" matching Zout = Zin is really wrong. |
| There is an ineradicable myth. The output impedance of the amplifier is always a tenth or a hundredth of the value of the loudspeaker impedance. The value of the output impedance of the amplifier Zsource is always hidden in the damping factor DF and can easily be calculated: Zsource = Zload / DF. Zload is the impedance of the loudspeaker. The cable resistance (impedance) is a part of the output impedance of the amplifier. Because of the high voltage of the source, cable screening (shielding) is not necessary in this case. The typical continuous query in the forums: "Can I use 4 ohm speakers to a 6 ohms amplifier?" (See reply under "Notice".) These issues show that there must be storytellers underway. How can we get rid of the nonsense of 2 to 16 ohms amplifiers? The output impedance of an amplifier Zout is always smaller than 0.5 Ohm. Zout << Zin. Amateurs are happy to speak of an 8 ohm amplifier, if they think not correctly that the amplifier output should be connected to "8 ohm speakers". Dealers use exactly these unclear expressions. In reality, the speaker impedance curve of a loudspeaker is never a straight line. Typical loudspeaker impedance curves vs. frequency |
| Studio parts | Output impedance Zsource |
Input impedance Zload |
| Microphone | 35 Ω to 200 Ω | − |
| Microphone preamplifier | − | 1 kΩ to 2 kΩ |
| Power amplifier | 0.01 Ω to 0.1 Ω | − |
| Loudspeaker | − | 2 Ω to 16 Ω |
| Studio gear (mixer) | 40 Ω | 10 kΩ to 20 kΩ |
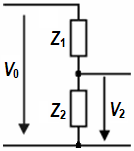
Impedances behave like an unloaded voltage divider. Zload = Z1and Zsource = Z2.
| Signal loss in dB: 20 log [Z1 / (Z1 + Z2)] Damping factor: DF = Z1 / Z2 Source impedance in ohms: Z2 = Z1 / DF |
Please enter two values, the third value will be calculated.
Please tell your friends: There are really no 4 or 8 ohms amplifiers to match the speakers.
Interconnection of two audio units equals a circuit of a voltage divider − Z2 << Z1.
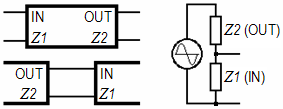
Attention: The numbering of the impedances is inversely to a voltage divider.
The two impedances Z1 and Z2 at one device
The damping factor is usually given as numerical value, but also in decibels.
| Enter a value in the left or right box. The calculator works in both directions of the ↔ sign. |
Calculation of the damping factor
| How do I calculate the damping factor DF for example, at 1 kHz, if neither the impedance of
the source Z2 nor the impedance of the load Z1 is known? Allow the source to send out of a 1 kHz sine tone and measure the resulting voltageV0 at the output without any load. Then measure at this point the voltage VL, when the load is applied. The damping factor is: (V0 − VL) is the voltage drop by the connected load. |
Calculation: Cable Length, Cable Capacitance, and Treble Loss (Cutoff Frequency)
 |
|
Effect of the input impedance on guitar amps
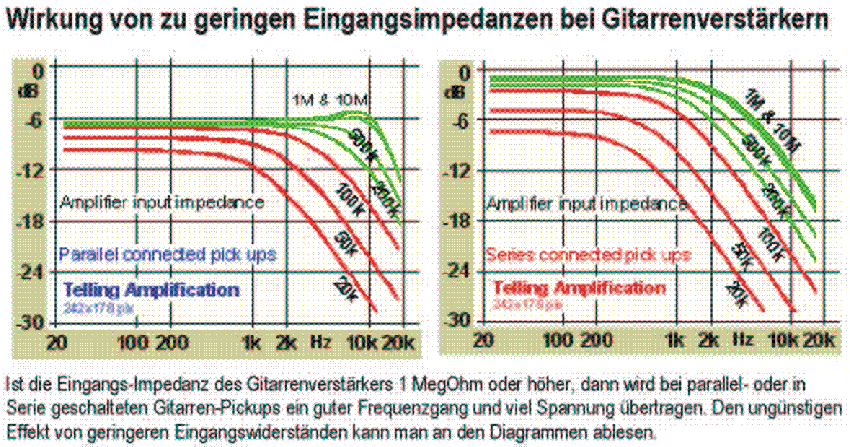 |
Influence of the amplifier impedance on the guitar pick-up
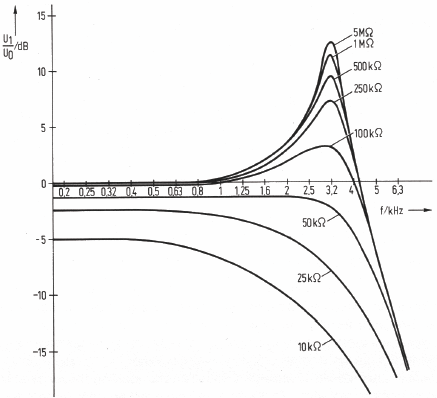 |
| back |
Search Engine |
home |