dB chart voltage power table conversion sound pressure sound intensity decibel voltage level levels ratio dbu dBA dBm absolute relative acoustic measurement volts watts and pascals database

Relative level − decibel chart
and dB conversion calculator

Conversion of voltage or power ratios to decibels dB
Table and chart − volts, watts, and pascals, W/m²

The dB calculator - a valuable tool

The sound pressure variation is the instantaneous acoustic pressure as RMS value.

Voltage or sound pressure ratio	Power or intensity ratio	← − dB + →	Voltage or sound pressure ratio	Power or intensity ratio
1.000	1.000	0	1.000	1.000
0.989	0.977	0.1	1.012	1.023
0.977	0.955	0.2	1.023	1.047
0.966	0.933	0.3	1.035	1.072
0.955	0.912	0.4	1.047	1.096
0.944	0.891	0.5	1.059	1.122
0.933	0.871	0.6	1.072	1.148
0.923	0.851	0.7	1.084	1.175
0.912	0.832	0.8	1.096	1.202
0.902	0.813	0.9	1.109	1.230
0.891	0.794	1.0	1.122	1.259
0.841	0.708	1.5	1.189	1.413
0.794	0.631	2.0	1.259	1.585
0.750	0.562	2.5	1.334	1.778
0.707	0.501	3.0	1.413	1.995
0.668	0.447	3.5	1.496	2.239
0.631	0.398	4.0	1.585	2.512
0.596	0.355	4.5	1.679	2.818
0.562	0.316	5.0	1.778	3.162
0.531	0.282	5.5	1.884	3.548
0.501	0.250	6.0	1.995	4.000
0.473	0.224	6.5	2.113	4.467
0.447	0.200	7.0	2.239	5.012
0.422	0.178	7.5	2.371	5.623
0.398	0.159	8.0	2.512	6.310
0.376	0.141	8.5	2.661	7.079
0.355	0.126	9.0	2.818	7.943
0.335	0.112	9.5	2.985	8.913
0.316	0.100	10	3.162	10.00
0.282	0.0794	11	3.55	12.6
0.251	0.0631	12	3.98	15.8
0.224	0.0501	13	4.47	20.0
0.199	0.0398	14	5.01	25.1
0.178	0.0316	15	5.62	31.6
0.159	0.0251	16	6.31	39.8
0.141	0.0200	17	7.08	50.1
0.126	0.0159	18	7.94	63.1
0.112	0.0126	19	8.91	79.4
0.100	0.0100	20	10.0	100.0
3.16×10⁻²	10⁻³	30	3.16×10	10³
10⁻²= 0.01	10⁻⁴	40	10² = 100	10⁴
3.16×10⁻³	10⁻⁵	50	3.16×10²	10⁵
10⁻³ = 0.001	10⁻⁶	60	10³ = 1000	10⁶
3.16×10⁻⁴	10⁻⁷	70	3.16×10³	10⁷
10⁻⁴	10⁻⁸	80	10⁴	10⁸
3.16×10⁻⁵	10⁻⁹	90	3.16×10⁴	10⁹
10⁻⁵	10⁻¹⁰	100	10⁵	10¹⁰
3.16×10⁻⁶	10⁻¹¹	110	3.16×10⁵	10¹¹
10⁻⁶	10⁻¹²	120	10⁶	10¹²

Field quantity (size) − Voltage

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Energy quantity (size) − Power

For dBm it was decided the reference power P₁ or P₀ = 1 milliwatt = 0.001 watt (≡ 0 dB).

Electric power (telephone) P watts	↔	Electric Power level L_P dB_m

Reference power P₀ = 1 milliwatt (mW) = 0.001 W ≡ 0 dB_m


Level of field quantities		Level of energy quantities

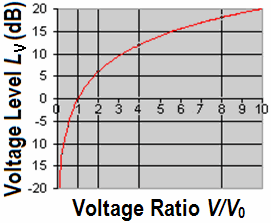
We are mainly concerned with conditions of sound pressure,
sound velocity, and audio voltage that are field quantities.
Voltage level is: L_V = 20 × log₁₀(V₁ / V₀)
Voltage is: V₁ = V₀ × 10^{(LV / 20)}
Reference voltage V₀ = 1 Volt.

Sound Field Quantities

Sound pressure, sound or particle velocity,
particle displacement or displacement amplitude,
(voltage, current, electric resistance).
Inverse Distance Law 1/r

Sound Energy Quantities
Sound intensity, sound energy density,
sound energy, acoustic power.
(electrical power).
Inverse Square Law 1/r²

Decibel scale for linear field quantities, like volts and sound pressures

The logarithmic scale (ratio)

Comparison of sound pressure level SPL and sound intensity level

Absolute level − dB chart

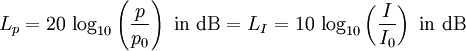referred to 0.7746 volt in dBu and to 1 volt in dBV

Conversion of decibel to voltage re 0.7746 volt and re 1 volt

Voltage re 0.7746 volt	Voltage re 1 volt	← − dB + →	Voltage re 0.7746 volt	Voltage re 1 volt
0.775	1.000	0	0.775	1.000
0.766	0.989	0.1	0.784	1.012
0.757	0.977	0.2	0.793	1.023
0.748	0.966	0.3	0.802	1.035
0.740	0.955	0.4	0.811	1.047
0.731	0.944	0.5	0.820	1.059
0.723	0.933	0.6	0.830	1.072
0.715	0.923	0.7	0.840	1.084
0.706	0.912	0.8	0.849	1.096
0.698	0.902	0.9	0.859	1.109
0.690	0.891	1.0	0.869	1.122
0.652	0.841	1.5	0.921	1.189
0.615	0.794	2.0	0.975	1.259
0.581	0.750	2.5	1.033	1.334
0.548	0.707	3.0	1.095	1.414
0.518	0.668	3.5	1.159	1.496
0.489	0.631	4.0	1.228	1.585
0.461	0.596	4.5	1.300	1.679
0.436	0.562	5.0	1.377	1.778
0.411	0.531	5.5	1.459	1.884
0.388	0.501	6.0	1.549	1.995
0.367	0.473	6.5	1.637	2.113
0.346	0.447	7.0	1.734	2.239
0.327	0.422	7.5	1.837	2.371
0.308	0.398	8.0	1.946	2.512
0.291	0.376	8.5	2.061	2.661
0.275	0.355	9.0	2.183	2.818
0.259	0.335	9.5	2.312	2.985
0.245	0.316	10	2.449	3.162
0.218	0.282	11	2.748	3.548
0.195	0.250	12	3.084	3.981
0.173	0.224	13	3.460	4.467
0.155	0.199	14	3.882	5.012
0.138	0.178	15	4.356	5.623
0.123	0.159	16	4.887	6.310
0.109	0.141	17	5.484	7.079
0.097	0.129	18	6.153	7.943
0.086	0.112	19	6.904	8.912
0.077	0.100	20	7.746	10.000
2.450×10⁻²	3.162×10⁻²	30	24.50	31.62
7.746×10⁻³	10⁻²	40	77.46	10²
2.450×10⁻³	3.162×10⁻³	50	2.450×10²	3.162×10²
7.746×10⁻⁴	10⁻³	60	7.746×10²	10³
2.450×10⁻⁴	3.162×10⁻⁴	70	2.450×10³	3.162×10³
7.746×10⁻⁵	10⁻⁴	80	7.746×10³	10⁴
2.450×10⁻⁵	3.162×10⁻⁵	90	2.450×10⁴	3.162×10⁴
7.746×10⁻⁶	10⁻⁵	100	7.746×10⁴	10⁵
2.450×10⁻⁶	3.162×10⁻⁶	110	2.450×10⁵	3.162×10⁵
7.746×10⁻⁷	10⁻⁶	120	7.746×10⁵	10⁶

Audio voltage and level

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Note - Comparing dBSPL and dBA:
            There is no conversion formula for measured dBA
            values to sound pressure level dBSPL or vice versa.
            That is only possible measuring one single frequency.

There is no "dBA" curve given as threshold of human hearing.
Readings of a pure 1 kHz tone should be identical, whether weighted or not.

Pro audio equipment often lists an A-weighted noise spec
– not because it correlates well with our hearing – but because it
can "hide" nasty hum components that make for bad noise specs.

Words to bright minds: Always wonder what a manufacturer
is hiding when they use A-weighting. *)

*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0

Sound measuring (Noise measuring) with weighting filter A and C

If the output voltage level is 0 dB, that is 100%, the level of −3 dB
is equivalent to 70.7% and the level of −6 dB is equivalent to 50%
of the initial output voltage.
This applies to all field quantities; e.g. sound pressure.

If the output power level is 0 dB, that is 100%, the level of −3 dB
is equivalent to 50% and −6 dB is equivalent to 25% of the initial
output power.
This applies to all energy quantities; e.g. sound intensity.

Try to understand this.

Different equations in books −
RMS or peak value?

The sound intensity I in W/m² in a plane progressive wave is given as:

or also as

But only one equation can be correct.

Sometimes, these equations will show further information: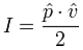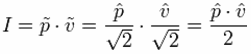

or also as formula

The tilde will indicate that it is the RMS value and the roof will show that it is the
amplitude value, ie, the peak value. For sinusoidal signals, the peak value means
the amplitude.
With these more accurate data, both equations are correct. You just need to know
exactly whether the peak value or the RMS value is applied.

Sound pressure p in Pa = N/m² − particle velocity v in m/s − acoustic intensity I in
N/m² · m/s = W/m² Energy equivalent: J (joule) = N · m = W · s

In audio engineering we always assume RMS values, if not specially noted different.

Simple rule of thumb: When working with power, 3 dB is twice, 10 dB is 10 times.
When working with voltage or current, 6 dB is twice, 20 dB is 10 times

back

Search engine

home

Voltage ratio V ratio = V₂/V₁	↔	Voltage level L_V dB

Voltage ratio 1 ≡ 0 dB at reference V_in = 1 volt

Power ratio P ratio = P₂/P₁	↔	Power level L_P dB

*Power ratio 1 ≡ 0 dB at reference P_in* = 1 watt**

Voltage V (audio) volts	↔	Voltage level L_u dBu
$V = V_0 \cdot 10^\frac{L_V}{20} \ \mbox{volts}$		$L_V = 20\, \log_{10}\left(\frac{V}{V_0}\right) \ \mbox{dBu}$
Reference voltage V₀ = 0.7746 Volt ≡ 0 dBu

Voltage V volts	↔	Voltage level L_V dBV
$V = V_0 \cdot 10^\frac{L_V}{20} \ \mbox{volts}$		$L_V = 20\, \log_{10}\left(\frac{V}{V_0}\right) \ \mbox{dBV}$
Reference voltage V₀ = 1 Volt ≡ 0 dBV