

| Deutsche Version |
|
This calculator is to determine the speed of sound in humid or moist air (water vapor) according to Owen
Cramer, "JASA, 93, p. 2510, 1993", with saturation vapor pressure taken from Richard S. Davis, "Metrologia,
29, p. 67, 1992", and a mole fraction of carbon dioxide of 0.0004. The calculator is valid over the temperature range 0 to 30°C (273.15 to 303.15 K) and over the pressure range 75 to 102 kPa. In the region between the air pressures 95 and 104 kPa there is no noticeable changing of the speed of sound c. The standard air pressure (atmospheric pressure) is 101325 Pa = 101.325 kPa or 1013.25 hectopascal. |
| The speed of sound in air is determined by the air itself and is not dependent
upon the amplitude, frequency, or wavelength of the sound. For an ideal
gas the speed of sound depends only on its temperature and is independent
of gas pressure. This dependence also applies really good to air, in good
approximation and can be regarded as an ideal gas. Environmental effects change the speed of sound and the absorption of sound in air. Even seemingly small percentage changes may cause serious listening problems in enclosed acoustic spaces. The air pressure is entered here anyway, it could be that you have to involve a pressure far from normal. Don't forget, this is a site for sound designers. |
| Notice for musicians and technicians (not for professors of physics): The speed of sound changes clearly with temperature, a little bit with humidity − but not with air pressure (atmospheric pressure). The words "sound pressure at sea level" are incorrect and misleading in the case of "speed of sound". The temperature indication, however, is absolutely necessary. Changing of the air pressure does not change the sound of musical instruments in concert halls or in a rooms. Changing temperature does it. Because the air pressure can be entered into the computer, there is no contradiction. In the air pressure range between 98 and 104 kPa virtually no changes of the speed of sound arise. At the air pressure conditions in which a violinist or a clarinetist feels good, no noticeable changes in speed of sound are observed. |
| The average air pressure at sea level is 101325 Pa. However, this information is insignificant for the speed of sound. We always need the specification of the temperature. |
| Google is not correct (look at the following link) http://productforums.google.com/forum/#!category-topic/websearch/unexpected-search-results/N5JMdZOkeuQ Here is the answer of Google: "Speed of sound at sea level = 340.29 m/s". This is not a good answer, because they forgot to tell us the important temperature, and the given atmospheric pressure "at sea level" makes really no sense. |
| It is a wrong assumption that the speed of sound decreases
with altitude above sea level, because the density of air
decrease with height. The changing of atmospheric pressure
does not change the speed of sound. Only the colder temperature (!) lets decrease the speed of sound at higher altitudes. The speed of sound has nothing to do with "sea level" and sound pressure and without the medium air there is no speed of sound. |
| In SI units with dry air at 20°C (68°F), the speed of sound c is 343 meters per second (m/s). This also equates to 1235 km/h, 767 mph, 1125 feet per second (ft/s), or 666 knots. 767.3 miles per hour (mph), 12.79 miles per minute (mi/min), 0.2131 miles per second (mi/s). That is 0.343 kilometers per second (km/s), or 20.58 kilometers per minute (km/min). At the temperature of ϑ = 0°C the speed of sound in dry air was determined to be c = 331.3 m/s. 0°C equals 68°F. It makes no sense to give the speed of sound adding the words at the "standard atmosphere at sea level". To get the speed of sound the temperature is important, not the barometric pressure. Statement: The static air pressure p_ and the density ρ of air (air density) are proportional at the same temperature. The ratio p_ / ρ is always constant, on a high mountain or even on sea level altitude. |
Speed of sound 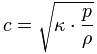 |
| That means, the ratio p_ / ρ is always constant on a high mountain, and even at "sea level". The static atmospheric pressurep_ and the density of air ρ go always together. The ratio stays constant. When calculating the speed of sound forget the atmospheric pressure, but look accurately at the very important temperature. The speed of sound varies with altitude (height) only because of the changing temperature there. Pressure is dependent on temperature and indirectly on altitude. |
| The speed of sound is called Mach 1 Mach is commonly used to represent an object's speed, such as an aircraft or a missile, when it is travelling at the speed of sound or at multiples of it. The speed higher than Mach 1 is called supersonic speed. |
| Mach number below 1 means the flow velocity is lower than the speed of sound - and the speed is subsonic. Mach number 1 means the flow velocity is the speed of sound - and the speed around that is transonic. Mach number above 1 means the flow velocity is higher than the speed of sound - and the speed is supersonic. More than Mach number 5 is called hypersonic. The "Mach number" is a dimensionless ratio. |
| M < 1: Subsonic flow M = 1: Sonic flow M > 1: Supersonic flow |
| Mach number | M < 0.3 | 0.3 < M < 1 | M = 1 | M ≈ 1 | 1 < M < 5 | 5 < M |
| Name | Low subsonic | High subsonic | Sonic | Transonic | Supersonic | Hypersonic |
| Note: The speed of sound c is independent of the frequency and the amplitude of the sound wave and the air pressure. But the speed of sound is dependent on the temperature. |
| The supersonic speed has absolutely nothing to do with the air pressure - but with the temperature! The density ρ of the air also has no effect, because the ratio of the air pressure p_ to the density ρ that is p_ / ρ is always constant. Look at this formula:
|
| Frequency dependent attenuation of air (dB) in 30 m distance at different humidity (percent) |
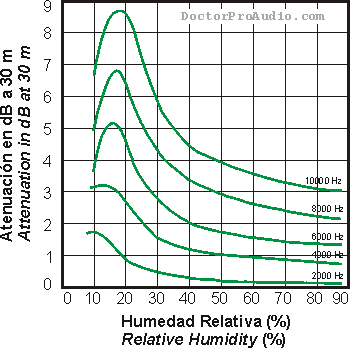 |
| Image used with kind permission of DoctorProAudio.com The consistency of the humidity level is important, when making recordings. There is no ideal humidity. |
Air Density Calculations
First, consider the ideal gas law:
(1) p · V = n · R · T
| p = pressure, pascals (multiply mb by 100 to get pascals) |
| V = volume in m3 |
| n = number of moles |
| R = specific gas constant |
| T= temperature K = °C + 273.15 |
Density D = ρ is the number of molecules of the ideal gas in a certain volume.
In this case a molar volume, which can be mathematically expressed as:
(2) D = ρ = n / V
| D = ρ = density in kg/m3 |
| n = number of molecules |
| V = volume in m3 |
By combining the previous two equations, the expression for the density D = ρ becomes:
(3) ![]()
| D = ρ = density in kg/m3 |
| p = pressure, pascals (multiply mb by 100 to get pascals) |
| R =specific gas constant = 287.058 J / (kg · K) for dry air |
| T = temperature K = °C + 273.15 |
As an example, using the standard sea level conditions of P = 101325 Pa and T = 15°C,
the air density at sea level, can be calculated as:
D = ρ = 101325 / (287.058 × (15 + 273.15)) = 1.2250 kg/m3
This example has been derived for the dry air of the standard conditions. For real-world situations,
it is necessary to understand how the density is affected by the moisture in the air.
The density D = ρ of a mixture of dry air molecules and water vapor molecules can be expressed as:
(4) ![]()
| D = ρ = density in kg/m3 |
| pd = pressure of dry air in pascals |
| pv = pressure of water vapor in pascals |
| Rd = specific gas constant for dry air = 287.05 J / (kg · K) |
| Rv = gas constant for water vapor 461.495 J / (kg · K) |
| T = temperature K = °C + 273.15 |
To determine the density of the air, it is necessary to know the actual air pressure, also
known as absolute pressure, or station pressure, the water vapor pressure, and the temperature.
| Conversion of dB between air to water |
| In 1970, the pressure reference level of 0 dB ≡ 1 µPa was chosen by the US Navy for their underwater work for sound in water. Approximately the same level of detail for air and water at their respective reference pressure in level differ by approximately 62 dB. So withdraw from the sound level of water about 62 dB to compare with sound level of air. |
| Calculation of the wavelength with frequency and temperature Speed of sound - temperature matters, not air pressure Calculation of the wavelength of radio waves and acoustic waves |
The speed of sound in water is approximately 1500 m/s. It is possible to measure changes
in ocean temperature by observing the resultant change in speed of sound over long distances.
The speed of sound in an ocean is approximately:
c = 1449.2 + 4.6 × T - 0.055 × T2 + 0.00029 × T3 + (1.34 - 0.01 × T) · (s - 35) + 0.0163 × z
T = temperature in degrees Celsius
s = salinity in parts per thousand
z = depth in meters
Table (chart): The impact of temperature
The air density, the speed of sound, the characteristic acoustic
impedance and the dependency of the temperature of air
| Temperature of air ϑ in °C |
Speed of sound c in m/s |
Time per 1 m Δ t in ms/m |
Density of air ρ in kg/m3 |
Impedance of air Z0 in N·s/m3 |
| +40 | 354.94 | 2.817 | 1.1272 | 400.0 |
| +35 | 351.96 | 2.840 | 1.1455 | 403.2 |
| +30 | 349.08 | 2.864 | 1.1644 | 406.5 |
| +25 | 346.18 | 2.888 | 1.1839 | 409.4 |
| +20 | 343.26 | 2.912 | 1.2041 | 413.3 |
| +15 | 340.31 | 2.937 | 1.2250 | 416.9 |
| +10 | 337.33 | 2.963 | 1.2466 | 420.5 |
| +5 | 334.33 | 2.990 | 1.2690 | 424.3 |
| 0 | 331.30 | 3.017 | 1.2920 | 428.0 |
| −5 | 328.24 | 3.044 | 1.3163 | 432.1 |
| −10 | 325.16 | 3.073 | 1.3413 | 436.1 |
| −15 | 322.04 | 3.103 | 1.3673 | 440.3 |
| −20 | 318.89 | 3.134 | 1.3943 | 444.6 |
| −25 | 315.72 | 3.165 | 1.4224 | 449.1 |
ϑ = Temperature, c = Speed of sound, ρ = Density of air, Z0 = ρ × c = Specific acoustic impedance of air
Sound pressure p = √ (I × Z0) and Sound intensity I = p² / Z0 ρ = 101325 / (287.058 × (273.15 + ϑ))
Standard air pressure p0 = 101325 Pa, Specific gas constant R = 287.058 J/kg × K.
Notice: Air pressure p and air density ρ are not the same.
In gases, the higher the velocity of sound, the higher the pitch will be, when you sing.
Only because of the decreasing air temperature, which decreases with altitude, the speed of sound decreases.
| Sometimes it is incorrectly assumed that the air pressure and air density are the same. The speed of sound c is not the particle velocity v. The sound velocity v is better called particle velocity v. The velocity of sound c is better called speed of sound c. |
Calculation and conversion: Temperature and Speed of Sound
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| Sound waves and electromagnetic waves are different. Sound waves need a medium to travel through, while the electromagnetic waves do not. The properties of a sound wave depend on the properties of the medium it travels through. |
The speed of sound in water
The speed of sound in water is about 1480 m/s. It is possible to measure changes in ocean temperature
by determining the speed of sound over long distances. The speed of sound in ocean water is about:
![]()
where T is the temperature in degrees Celsius (°C), S is the salinity in psu and D is the depth in meters.
Change of speed of sound with the change in height
| The standard table: Speed of Sound at Different Altitudes The speed of sound is not a constant, but depends actually on the temperature at that altitude. The statement that the speed of sound is related to the height above ground is not correct. The speed of sound changes only with temperature. Sure, it's just very cold up there. |
Change of air pressure associated with the change in height
| Question: How does the air pressure change if the height changes 1 meter? The hydrostatic pressure is calculated according to Blaise Pascal: This law is also assumed for an air column. Height h = 1 m Standard gravitational acceleration is g = 9.80665 m/s2 Density of air at 20°C is ρ20 = 1.204 kg/m3 1 m height changes the air pressure at a constant temperature of 20°C by p = ρ20 ∙ g ∙ h = 1.204 kg/m3 × 9.80665 m/s2 × 1 m = 11.8 Pa (N/m²) Rule of thumb: At ground level the air pressure decreases by 1 hPa = 100 Pa with change of altitude of h = 8.5 meters. But the temperature has a tendency to decrease with height. |
Converter: Fahrenheit to Celsius and Celsius to Fahrenheit
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |

| back |
Search Engine |
home |