

| Deutsche Version |
| It is a wrong assumption that the speed of sound decreases with altitude above sea level, because the density of air decreases with height. The changing of atmospheric pressure does not change the speed of sound. Only the colder temperature (!) lets decrease the speed of sound at higher altitudes. The speed of sound has nothing to do with "sea level". For sound pressure without the medium air there is no speed of sound. Speed of sound is dependent nearly only on its temperature. It is not dependent on the sound amplitude, frequency, or wavelength. |
| At 0°C is ρ0 = 1.293 kg/m3, Z0 = 428 N·s/m3, and c0 = 331.3 m/s At 15°C is ρ15 = 1.225 kg/m3, Z15 = 417 N·s/m3, and c15 = 340 m/s At 20°C is ρ20 = 1.204 kg/m3, Z20 = 413 N·s/m3, and c20 = 343 m/s At 25°C is ρ20 = 1.184 kg/m3, Z25 = 410 N·s/m3, and c25 = 346 m/s |
| The speed of sound in air c is determined by the air itself and is not dependent upon the amplitude, frequency, or wavelength of the sound. For an ideal gas the speed of sound depends only on its temperature and is independent of gas pressure. This dependence also applies to air, in good approximation and can be regarded as an ideal gas. This is a site for sound engineers and musicians. We are interested in the speed of sound of air (!) on Earth at places where acoustic musical instruments or voices are used, usually in rooms or halls. The speed of sound of atmospheric layers, as in 100 km altitude (height), or close to the vacuum is not of interest. Also we do not care about higher air pressure in car tires. Which speed does sound in our usual life have? |
| Notice for musicians and technicians (not for professors of physics): The speed of sound in air changes clearly with temperature, a little bit with humidity − but not with air pressure (atmospheric pressure) and height. The words "sound pressure at sea level" are incorrect and misleading in the case of "speed of sound". The temperature indication, however, is absolutely necessary. The changing of atmospheric pressure does not change the sound of musical instruments in a concert hall or in a room. That does the changing of temperature. |
| The average air pressure at sea level is 101325 Pa. However, this information is insignificant for the speed of sound. We always need the specification of the temperature. |
| Google is not correct (look at the following link) http://productforums.google.com/forum/#!category-topic/websearch/unexpected-search-results/N5JMdZOkeuQ Here is the answer of Google: "Speed of sound at sea level = 340.29 m/s". This is not a good answer, because someoneto forgot to tell us the important temperature, and the given atmospheric pressure "at sea level" makes really no sense. |
| In SI units with dry air at 20°C (68°F), the speed of sound c is 343 meters per second (m/s). This also equates to 1235 km/h, 1125 feet per second (ft/s or fps), 666 knots, 767.3 miles per hour (mi/h or mph), 12.79 miles per minute (mi/min), 0.2131 miles per second (mi/s), That is 0.343 kilometers per second (km/s), or 20.58 kilometers per minute (km/min). It makes no sense to give the speed of sound adding the words at the "standard atmosphere at sea level". To get the speed of sound the temperature is important, not the barometric pressure. Statement: The static air pressure p_ and the density ρ of air (air density) are proportional at the same temperature, because the ratio p_ / ρ is always constant, on a high mountain or even on sea level altitude. Notice: The ratio p_ / ρ (static air pressure to air density) is really always constant. Formula: |
Speed of sound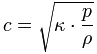 |
| That means, the ratio p_ / ρ is always constant on a high mountain, and even at "sea level". The static atmospheric pressurep_ and the density of air ρ go always together. The ratio stays constant. When calculating the speed of sound forget the atmospheric pressure, but look accurately at the very important temperature. The speed of sound varies with altitude (height) only because of the changing temperature there. Pressure is dependent on temperature and indirectly on altitude. |
| Adiabatic index or ratio of specific heats κ (kappa) = cp / cv = 1.402 for air. Specific heat in a constant pressure process = cp; Specific heat in a constant volume process = cv Generally we take with sufficient accuracy the formula (equation) for the speed of sound in air in m/s vs. temperature ϑ (theta) in degrees Celsius (centigrade):
That gives e.g. at a temperature of ϑ = 20°C a speed of sound of: c ≈ 331.3 + (0.6 × ϑ) = 331.3 + (0.6 × 20) = 343.3 m/s.
There is a useful formula (rule of thumb) to get the temperature ϑ in °C when you know the speed of sound c in air (m/s). Formula: Temperature of air ϑ ≈ (c − 331.3) / 0.6 in °C. With the following formula you can calculate exactly the speed of sound. Speed of sound 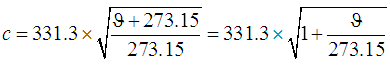 in m/s; in m/s;temperature ϑ in °C. |
Speed of sound vs height and temperature?
Forget the height and take care only about the temperature.
| At the temperature of ϑ = 0°C the speed of sound in dry air was determined to be c = 331.3 m/s. 0°C equals 32°F. Exact equations for speed of sound and temperature: To calculate accurately the speed of sound in m/s: c = 331.3 × √ (1+(ϑ / 273.15)) if one uses the known temperature of air ϑ in °C. To calculate accurately the temperature of air in °C: ϑ = 273.15 × (0.0000091108129040816350702156684298215 × c2 − 1) if one uses the known speed of sound c in m/s. Simplified formulas (for +35°C to −35°C): Speed of sound in air in m/s: c = 331.3 + 0.6 × ϑ Temperature in °C: ϑ = (c − 331.3) / 0.6 |
Calculation and conversion: Temperature and speed of sound
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| The speed of sound c depends on the temperature of air ϑ and not on the air pressure! The humidity of air has some negligible effect on the speed of sound. The air pressure and the density of air (air density) are proportional to each other at the same temperature. It applies always p / ρ = constant. rho is the density ρ and p is the sound pressure. Therefore air pressure does not enter the calculation of the speed of sound of air. |
| Notice: The speed of sound is alike on a mountain top as well as at sea level, provided that there is the same air temperature. It can be assumed that this is true even at 100 km altitude. With decreasing pressure, the density of air decreases. |
At what temperature the speed of sound is double its value of 0°C?
| At which temperature the speed of sound 331.3 m/s (velocity of sound) will be doubled? A temperature of 819.45°C will double the speed of sound to 662.6 m/s. |
| Look for the following answer of the question: "What is the speed of sound?" Speed of sound - temperature matters, not air pressure Density of air (air density) ρ = air pressure p_ ÷ (gas constant R × temperature in Kelvin) ρ = p_ / R × T in kg/m3. The specific gas constant for dry air is R = 287.058 J/kg×K Joule J = newton × meter = N·m and T in Kelvin = °C + 273.15 Atmospheric pressure p0 = 101325 Pa = 1013.25 mbar = 1013.25 hPa R = 287.058 J/kg×K T0 = 273.15 K at 0°C ρ0 = 101325 / (287.058 × 273.15) = 1.2922 kg/m³ T20 = 293.15 K at 20°C ρ20 = 101325 / (287.058 × 293.15) = 1.2041 kg/m³ Sometimes it is incorrectly assumed that the air pressure and air density are the same. The speed of sound c is not the particle velocity v. The sound velocity v is better called particle velocity v. The velocity of sound c is better called speed of sound c. |
| The speed of sound is called Mach 1 Mach is commonly used to represent an object's speed, such as an aircraft or a missile, when it is travelling at the speed of sound or at multiples of it. The speed higher than Mach 1 is called supersonic speed. |
| Mach number below 1 means the flow velocity is lower than the speed of sound - and the speed is subsonic. Mach number 1 means the flow velocity is the speed of sound - and the speed around that is transonic. Mach number above 1 means the flow velocity is higher than the speed of sound - and the speed is supersonic. More than Mach number 5 is called hypersonic. The "Mach number" is a dimensionless ratio. |
| Note: The speed of sound c is independent of the frequency and the amplitude of the sound wave, and the air pressure. But the speed of sound is dependent on the temperature. At a temperature of 819.45, we get a speed of sound of 662.6 m/s. That is double the speed of sound, we find at 0°C with 331.3 m. |
| The supersonic speed has absolutely nothing to do with the air pressure – but with the temperature! The density ρ of the air also has no effect, because the ratio of the air pressure p to the density ρ that is p / ρ is always constant. Look at this important formula:
|
Table (chart): The impact of temperature
The air density, the speed of sound, the characteristic acoustic
impedance and the dependency of the temperature of air
| Temperature of air ϑ in °C |
Speed of sound c in m/s |
Time per 1 m Δ t in ms/m |
Density of air ρ in kg/m3 |
Impedance of air Z in N·s/m3 |
| +40 | 354.94 | 2.817 | 1.1272 | 400.0 |
| +35 | 351.96 | 2.840 | 1.1455 | 403.2 |
| +30 | 349.08 | 2.864 | 1.1644 | 406.5 |
| +25 | 346.18 | 2.888 | 1.1839 | 409.4 |
| +20 | 343.26 | 2.912 | 1.2041 | 413.3 |
| +15 | 340.31 | 2.937 | 1.2250 | 416.9 |
| +10 | 337.33 | 2.963 | 1.2466 | 420.5 |
| +5 | 334.33 | 2.990 | 1.2690 | 424.3 |
| 0 | 331.30 | 3.017 | 1.2920 | 428.0 |
| −5 | 328.24 | 3.044 | 1.3163 | 432.1 |
| −10 | 325.16 | 3.073 | 1.3413 | 436.1 |
| −15 | 322.04 | 3.103 | 1.3673 | 440.3 |
| −20 | 318.89 | 3.134 | 1.3943 | 444.6 |
| −25 | 315.72 | 3.165 | 1.4224 | 449.1 |
Notice: Air pressure p and air density ρ are not the same.
In gases, the higher the speed of sound in that medium, the higher the pitch will be, when you sing.
Only because of the decreasing air temperature, which decreases with altitude (height), the speed of sound decreases.
In conventional use and in scientific literature sound velocity is the same as speed of sound or acoustic velocity.
Sound velocity c should not be confused with sound particle velocity v, which is the velocity of the individual particles.
| Approximate speed of sound in common materials |
|||
| Medium | Speed of sound m/s ft/s |
||
| Air, dry at 20°C | 343 | 1 125 | |
| Hydrogen at 0°C | 1 280 | 4 200 | |
| Water at 15 °C | 1 500 | 4 920 | |
| Lead | 2 160 | 7 090 | |
| Concrete | 3 100 | 10 200 | |
| Wood (soft - along the fibre) | 3 800 | 12 500 | |
| Glass | 5 500 | 18 500 | |
| Steel | 5 800 | 19 000 | |
| In a given ideal gas the speed of sound depends only on its temperature. The speed of sound in still dry air at a temperature of ϑ = 0 degrees Celsius is c = 331.3 m/s. It depends on the temperature and material. Since sound is transferred easily through densely packed molecules, it is faster in denser substances. Thus the speed of sound increases with the stiffness of the material. |
| On the frequent question: "How much is the speed of sound?" must always follow the demand: "At what temperature, please?" Who mentions the barometric pressure, has still something to learn. |
Speed of sound and acoustic velocity (velocity of sound)
| Speed is the rate of change of distance with time. Velocity is a measure of both speed and direction of a moving object. Velocity is the rate of change of displacement with time. Speed is a distance an object goes, velocity is measurement of speed AND direction. |
|
In a given ideal gas the sound speed depends only on its temperature. The speed of sound in still air at 0 degrees Celsius is 331.3 m/s. It depends on the temperature, and the material. Since sound is more easily transmitted between close molecules, it travels faster in the denser substance. Thus the speed of sound increases with the stiffness of the material. |
Really wrong answers at "Yahoo! Answers"
|
| Calculations and conversions of pressure units More conversions of pressure and stress units Conversions of pressure units |
Properties of sound in air, frequency and wavelength
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| At 0° Celsius the speed of sound in U.S. textbooks is 331.3 m/s. At 20° Celsius the speed of sound then is 343.21 m/s, rounded 343 m/s. At 0° Celsius, the speed of sound in German textbooks is 331.5 m/s. At 20° Celsius the speed of sound then is 343.42 m/s, rounded 343 m/s. |
Speed and Velocity - The Difference
| Speed is the distance in a certain period of time. Velocity is a measure of both speed and direction of a moving object. Difference: Speed is a distance an object goes in unit time. Velocity is displacement made in unit time. Difference: Speed is a scalar quantity – it has only magnitude and cannot be zero. Velocity is a vector quantity – it has both magnitude and direction and it can be zero. |
| Look at: Dennis A. Bohn, "Environmental Effects on the Speed of Sound" |
Converter: Fahrenheit to Celsius and Celsius to Fahrenheit
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
| Sound pressure or acoustic pressure is the local pressure deviation from the ambient atmospheric pressure caused by a sound wave. Sound pressure can be measured using a microphone in air. The SI unit for sound pressure p is the pascal − symbol: Pa. |
| NASA says: The speed of sound is dependent on the temperature of the air. It varies with altitude (height) only because of the changing temperature! The atmospheric pressure is proportional to the density of air. Therefore both values have no effect on the speed of sound. |
|
"Speed of sound":
http://www.grc.nasa.gov/WWW/k-12/airplane/sound.html "Speed of sound": http://www.grc.nasa.gov/WWW/BGH/sound.html "Atmos Modeler Simulator": http://www.grc.nasa.gov/WWW/k-12/airplane/atmosi.html "Variables that affect the speed of sound (Quicktime)": http://www.nasa.gov/audience/foreducators/topnav/materials/listbytype/Variables_That_Affect_the_Speed.html "Speed of Sound Derivation": http://www.grc.nasa.gov/WWW/BGH/snddrv.html "Mach number": http://www.grc.nasa.gov/WWW/k-12/airplane/mach.html |
| The speed of sound in air at 0°C can be calculated as c = (1.4×(287.058 J/K·kg)×(273.15 K))^1/2 = 331.3 m/s, where κ (kappa) = 1.4 and the specific gas constant for dry air R = 287.058 (J/K·kg). The speed of sound in air at 20°C can be calculated as c = (1.4×(287.058 J/K·kg)×(293.15 K))^1/2 = 343.24 m/s. |
| Zonal mean vertical profile of temperature in the atmosphere during June at 45° North  Temperature vs. Height (Atmospheric Pressure) |
| Wrong thinking: Calculate speed of sound at high elevations. You feel the assumption that this must have to do with height. That is wrong. Only the temperature has to do with the value of the speed of sound. It's pretty cold above there. |
| The sound pressure or acoustic pressure (alternating pressure changes) is a dynamic pressure. However, the air pressure (atmospheric equal pressure) is a static pressure. The dynamic sound pressure is superimposed on the static air pressure. |
| Note: Time, frequency and phase belong close together. The height of the amplitude has no influence on those parameters. The amplitude A has nothing to do with the frequency, the wavelength, the time duration and the speed of sound. |
| back |
Search Engine |
home |