

| Deutsche Version |
| The subjective perceived sound volume and the artificial term loudness are
subjective terms trying to describe the strength of the ear's perception of a sound. The determination of the loudness of stationary signals is defined in ISO 532 or in DIN 45631. |
| The loudness of N = 1 sone is equivalent to 40 phons, which is the loudness level of LN = 40 dB of a sine wave (sinusoid) with a frequency of f = 1000 Hz. Kurt Tucholsky: "Noise is the noise of others and one's dog makes no noise." "There are many kinds of noise - but only one silence." Loudness is a personal subjective characteristic of a sound - as opposed to the sound pressure level in decibels, which is objective and directly measurable. SPL. |
Conversion valid between 40 phons and 120 phons
That means for larger values than '1 sone is equal to 40 phons'
For loudness level LN > 40 phons: loudness N in sones = 2[(LN − 40)/10] (LN in phons)
For loudness N > 1 sone: loudness level LN in phons = 40 + [10 × log N / log102] (N in sones)
log 2 = 0.30103 LN in phons = 40 + 33.22 × log N N in sones
Conversion only valid between 8 phons and 40 phons
That means for smaller values than '1 sone is equal to 40 phons'
For loudness level LN < 40 phons: loudness N in sones = (LN / 40)2.86 − 0.005 LN in phons
For loudness N < 1 sone: loudness level LN in phons = 40 × (N + 0.0005)0.35 N in sones
| According to Stanley Smith Stevens' definition, 1 sone is equivalent to 40 phons,
which is defined as the loudness level of a pure 1 kHz tone at LN = 40 dBSPL,
but only (!) for a sine wave of 1 kHz and not for broadband noise. There is no "dBA" curve given as threshold of human hearing. "dBA" has absolutely noting to do with sone, or with phons, or sound pressure level in dB. 60 phons means "as loud as a pure 1000 Hz tone with a level of 60 dB." |
Relation between loudness N in sones
and loudness level LN in phons
 |
|
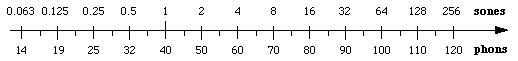 |
|
Loudness N (sone) and loudness level LN (phon), as shown here, is easily converted into one another. But the psychoacoustic perceived loudness level and the objectively measured sound pressure level in dBSPL cannot be converted to the weighted dBA level. There is no formula. The typical question: "How to convert 0.5 sone to decibel (dB)?" cannot be answered. Only a pure tone of 1 kHz measured in phons is equivalent to a dB-SPL value. Distinguish carefully when looking at the volume (magnitude of sound). Sone is part of the loudness. Phon is part of the loudness level. Try to avoid the laymen's word "intensity". dB or dB-SPL is the sound pressure level. dBA is a filter measurement for a very simplified evaluation of volume. |
| The volume of a sound is a subjective perception. To "measure" loudness,
the volume of a 1,000 hertz reference tone is adjusted until it is perceived by
listeners to be equally as loud as the sound being "measured". The loudness
level, in phons, of the sound is then equal to the sound-pressure level, in
decibels. Readings of a pure 1 kHz tone should be identical, whether
weighted or not. Between the loudness N in sone and the loudness level LN in phon we have the following connection (ISO-recommendation ISO/R 131-1959): Loudness N = 2(LN − 40)/10 or loudness level LN = 40 + 10 × lb N. "lb" means logarithm base 2. 10 × lb N = 10 × log2(N) The sone is a unit of perceived loudness after a proposal of Stanley Smith Stevens (1906-1973) in 1936. In acoustics, loudness is a subjective measure of the sound pressure. One sone is equivalent to 40 phons, which is defined as the loudness of a 1 kHz tone at 40 dBSPL. The number of sones to a phon was chosen so that a doubling of the number of sones sounds to the human ear like a doubling of the loudness, which also corresponds to increasing the sound pressure level by 10 dB, or increasing the sound pressure by a ratio 3.16 (= √10). At frequencies other than 1 kHz, the measurement in sones must be calibrated according to the frequency response of human hearing, which is of course a subjective process. The study of apparent loudness is included in the topic of psycho acoustics. Volume in acoustics is used as a synonym for loudness. It is a common term for the amplitude or the level of sound. To be fully precise, a measurement in sones must be qualified by the optional suffix G, which means that the loudness value is calculated from frequency groups, and by one of the two suffixes F (for free field) or D (for diffuse field). |
| Note - Comparing dB and dBA: There is no conversion formula for measured dBA values to sound pressure level dBSPL or vice versa. There is no correlation between sound pressure level SPL as broadband measuring and dBA. To know the measuring distance and the frequency content of the signals could also be important. |
| With the following table you can try to convert roughly, but be cautious using
these psychoacoustic values. The frequency composition of the signal
amplitude is always unknown. The distance of the measuring point is
important for the value of the measure. From a dB-A measurement no accurate description of the expected volume is possible. A typical noise question: How does dbA compare to sones? The following chart is, however, for the dBA values no accurate knowledge − it's more a guess. "Conversion" of "sones to dBA" |
Conversion between sones and phons −
but only a really rough "guess" for dBA values
| sones | phons | dBA | sones | phons | dBA | |
| 0.1 | 17.9 | 20.5 | 1.8 | 48.5 | 34.8 | |
| 0.2 | 22.8 | 21.5 | 1.9 | 49.3 | 35.3 | |
| 0.3 | 26.2 | 22.5 | 2.0 | 50.0 | 35.8 | |
| 0.4 | 29.0 | 23.5 | 2.1 | 50.7 | 36.4 | |
| 0.5 | 31.4 | 24.4 | 2.2 | 51.4 | 37.0 | |
| 0.6 | 33.5 | 25.3 | 2.3 | 52.0 | 37.5 | |
| 0.7 | 35.3 | 26.3 | 2.4 | 52.6 | 38.0 | |
| 0.8 | 37.0 | 27.2 | 2.5 | 53.2 | 38.4 | |
| 0.9 | 38.6 | 28.2 | 2.6 | 53.8 | 38.8 | |
| 1.0 | 40.0 | 29.2 | 2.7 | 54.3 | 39.3 | |
| 1.1 | 41.4 | 30.2 | 2.8 | 54.9 | 39.8 | |
| 1.2 | 42.6 | 31.1 | 2.9 | 55.4 | 40.2 | |
| 1.3 | 43.8 | 32.0 | 3.0 | 55.9 | 40.6 | |
| 1.4 | 44.9 | 32.9 | 3.1 | 56.3 | 41.1 | |
| 1.5 | 45.9 | 33.5 | 3.2 | 56.8 | 41.5 | |
| 1.6 | 46.9 | 33.9 | 3.3 | 57.2 | 42.0 | |
| 1.7 | 47.7 | 34.4 | 3.4 | 57.7 | 42.5 |
| Pro audio equipment often lists an A-weighted noise spec sheet − (specification) not because it correlates well with our hearing – but because it can "hide" nasty hum components that make for bad noise specs. Words to bright minds: Always wonder what a manufacturer is hiding when they use A-weighting. *) |
*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0
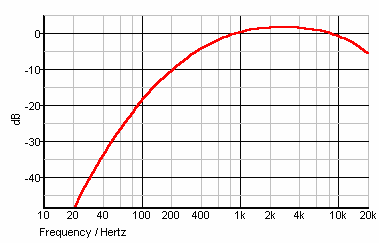 |
| This frequency weighting with the A-curve is used for noise measurements. It is close to the frequency response of the human hearing for levels below 40 dB only. But this filter is also used for higher levels, a purpose it was never intended for, and is not suited to, and therefore gives lower test results than our ears are hearing. The cut-off low frequencies are not measured. |
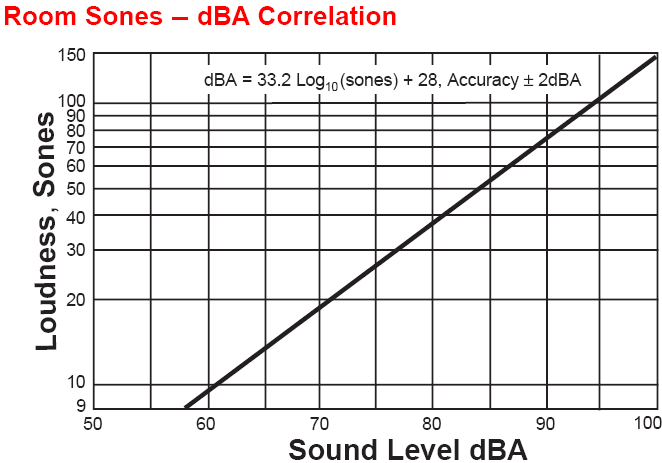
| A formula with a cautious try to convert sones to decibels: dBA = 33.22 × log (sones) + 28 with a possible accuracy of ± 2 dBA or sones = 10^[(dBA − 28) / 33.22] |
Weighting filter after DIN EN 61672-1 2003-10 (DIN-IEC 651) - weighted dBA and dBC
The phon is a unit of perceived loudness level, which is a subjective measure
of the strength (not intensity) of a sound. At a frequency of 1 kHz, 1 phon is
defined to be equal to 1 dB of sound pressure level above the nominal
threshold of hearing, the sound pressure level SPL of 20 µPa (micropascals) =
2×10−5 pascal (Pa). Our ears as sensors cannot convert sound intensities and
powers, they can only use the sound pressure changes between 20 Hz and
20,000 Hz. At other frequencies, the phon departs from the decibel, but is
related to it by a frequency weighting curve (equal-loudness contour) that
reflects the frequency response of human hearing. The standard curve for
human hearing is the A-weighted curve (the equal-loudness contour for a 40
dB stimulus at 1 kHz), but others are in use.
The "unit" phon has been largely replaced by the dBA (A-weighted decibel), though many old textbooks and instructors continue to use the phon. Note: "Set the volume of the radio double as loud or half as loud." Who does not know, how to do this, is a normal person. Psycho-acousticians are telling us, that it has to be 10 dB level difference. Try to cool your hot coffee to the point "half as hot" - and think it over. Your own feeling may be much different to other persons. An increase from 6 dB to 10 dB is perceived by most listeners as "double" the volume. These sensations are highly subjective, meaning that different people will hear this in different ways, and "twice as loud" is a much harder thing to guess than something. The human perception of loudness is perceived differently from each subject. In other words it is one's own perception of sound and it is subjective of sound pressure level SPL. |
| from the sound source (1/r²). This is an often-told and believed wrong tale. |
Sound Level Comparison Chart with Factor
| Table of sound level dependence and the change of the respective factor to subjective volume
(loudness), objective sound pressure (voltage), and sound intensity (acoustic power) How many decibels (dB) level change is double, half, or four times as loud? How many dB to appear twice as loud (two times)? Here are all the different factors. Factor means "how many times" or "how much" ... Doubling of loudness. |
| Level change |
Volume Loudness |
Voltage Sound pressure |
Acoustic Power Sound Intensity |
| +60 dB | 64 | 1000 | 1000000 |
| +50 dB | 32 | 316 | 100000 |
| +40 dB | 16 | 100 | 10000 |
| +30 dB | 8 | 31.6 | 1000 |
| +20 dB | 4 | 10 | 100 |
| +10 dB | 2.0 = double | 3.16 = √10 | 10 |
| +6 dB | 1.52 times | 2.0 = double | 4.0 |
| +3 dB | 1.23 times | 1.414 times = √2 | 2.0 = double |
| - - - - ±0 dB - - - - | - - -1.0 - - - - - - - | - - - - - 1.0 - - - - - - - | - - - - - 1.0 - - - - - - |
| −3 dB | 0.816 times | 0.707 times | 0.5 = half |
| −6 dB | 0.660 times | 0.5 = half | 0.25 |
| −10 dB | 0.5 = half | 0.316 | 0.1 |
| −20 dB | 0.25 | 0.100 | 0.01 |
| −30 dB | 0.125 | 0.0316 | 0.001 |
| −40 dB | 0.0625 | 0.0100 | 0.0001 |
| −50 dB | 0.0312 | 0.0032 | 0.00001 |
| −60 dB | 0.0156 | 0.001 | 0.000001 |
| Log. quantity | Psycho quantity | Field size | Energy size |
| dB change | Loudness multipl. | Amplitude multiplier | Power multiplier |
| For a 10 dB increase of the sound level we require ten times more power from the amplifier. This increase of the sound level means for the sound pressure a lifting of the factor 3.16. Loudness and volume are highly subjective. That belongs to the domain of psychoacoustics. |
| Is 10 dB or 6 dB sound level change for a doubling or halving of the loudness (volume) correct? About the connection between sound level and loudness, there are various theories. Far spread is still the theory of psycho-acoustic pioneer Stanley Smith Stevens, indicating that the doubling or halving the sensation of loudness corresponds to a level difference of 10 dB. Recent research by Richard M. Warren, on the other hand leads to a level difference of 6 dB. *) This means that a double sound pressure corresponds to a double loudness. The psychologist John G. Neuhoff found out that for the rising level our hearing is more sensitive than for the declining level. For the same sound level difference the change of loudness from quiet to loud is stronger than from loud to quiet. It is suggested that the sone scale of loudness reflects the influence of known experimental biases and hence does not represent a fundamental relation between stimulus and sensation. *) Richard M. Warren, "Elimination of Biases in Loudness Judgments for Tones", 1970, Journal of the Acoust. Soc. Am. Volume 48, Issue 6B, pp. 1397 - 1403 and Richard M. Warren, "Quantification of Loudness", 1973, American Journal of Psychology, Vol 86 (4), pp. 807 - 825 John G. Neuhoff, "An adaptive bias in the perception of looming auditory motion", 2001, Ecological Psychology 13 (2) pp. 87 - 110 and John G. Neuhoff, "Perceptual Bias for Rising Tones", 1998, Nature, Volume 395, September Citation: When known experimental biases were eliminated, half loudness was equal to half sound pressure level (−6 dB) from 45 to 90 dB. It follows that the determination of the volume (loudness) which is double as loud should not be dogmatically defined. More realistic is the claim: |
| A doubling of the sensed volume (loudness) is equivalent to a level change approximately between 6 dB and 10 dB, the psycho-acousticians are telling us. |
| How do you convert sound sizes to decibel values? How many decibels is twice (double, half) or three times as loud? How does the sound decrease with distance? |
| There is a constant uncertainty of the answer to the question: "How many dBs are doubling a sound"? or "What is twice the sound?" Doubling the (sound) intensity is obtained by an increase of the sound intensity level of 3 dB. Doubling the sound pressure is obtained by an increase of the sound pressure level of 6 dB ● Doubling the loudness feeling is obtained by an increase of the loudness level of about 10 dB. Double or twice the power = factor 2 means 3 dB more calculated power level (sound intensity level). Double or twice the voltage = factor 2 means 6 dB more measured voltage level (sound pressure level) ● Double or twice the loudness = factor 2 means 10 dB more sensed loudness level (psycho acoustic). |
|
A program to combine as much as ten (10) noise sources Conversion of sound pressure level to sound pressure and sound intensity |
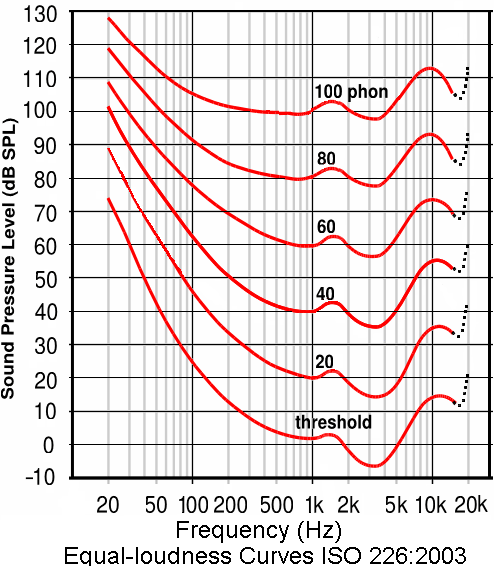
Curves of Equal-Loudness Level contours ISO 226 − The New Standard
Acoustics - Normal equal-loudness-level contours (ISO 226:2003)
| back |
Search Engine |
home |