Sound level distance damping decibel dB damping calculation calculator change distance versus sound level apps reduction drop dissipation SPL sound transmission loss free field loss sound and distance - decrease drop fall sound over distance versus dB sound different distances attenuation microphone calculator distance level drop ratio dampening

● Damping of sound level (decibel dB) vs. distance ●

Distance law − Distance damping − Noise − SPL

This is an approximation when the venue is a direct sound field or an anechoic chamber

How does the sound decrease with change of distance?
How do we calculate the distance drop of the noise?
How is the sound reduction in dB with distance?
How does distance affect sound (pressure)?
Sound and noise propagation and the level damping.
How far can sound travel? No frequency dependence

"Damping (attenuation) of air of high frequencies (dissipation)" is really a different fact.
Don't mix it up with the normal damping (decreasing) of sound with distance.

How do high frequencies affect sound? Frequency dependence.
How does distance affect sound? No frequency dependence.

The used browser does not support JavaScript.
You will see the program but the function will not work.

There is no noise decrease (sound reduction) or sound drop per meter.
We get a sound level drop of 6 dB per doubling of distance.

Sound power or sound power level has nothing to
do with the distance from the sound source.
Thinking helps: A 100 watt light bulb is emitting constantly the same power.
That is really the case - no matter if in 1 m, in 10 m, or even in 100 distance.
These emitted watts don't change with distance. They stay in the source.
Sound power is the distance independent cause of this, whereas sound
pressure is the distance-dependent effect.

Changing (decrease) of sound pressure level Δ L or sound pressure p
with distance r in a free field (direct field), like in anechoic chambers
Conversion: Distance values → dB level changing - The 1/r law for sound pressure
With sound level ususally a level of a logarithmic ratio of sound pressure is meant.

These calculations are meant only for sound engineers and the distance from point sources, like musicians or loudspeakers
to a microphone in a direct field - No air damping and frequency dependency of e.g. the thunder in a distance.

Avoid using the psychoacoustical terms loudness perception and volume.
This subjective sound-sensation is not clearly measurable without ambiguity.
The term "loudness" or "volume" is a problem because it belongs to psycho-
acoustics and this personal feeling is not correct definable.
Loudness as a psychological correlate of physical strength (amplitude) is also
affected by parameters other than sound pressure, including frequency,
bandwidth, spectral composition, information content, time structure, and the
duration of exposure of the sound signal. The same sound will not create the
same loudness perception by all individuals (people).

As psycho-acoustic parameters to describe the "loudness" there is the
"loudness level" with the unit phon and the "loudness" with the unit sone .

Incidentally, the sound pressure p doesn't decrease with the square of the distance
from the sound source (1/r²). This is an often-told and believed wrong tale.

Sound pressure level SPL depending on the distance
for point-shaped sound sources in the free field
● Distance-related decrease of sound level ●

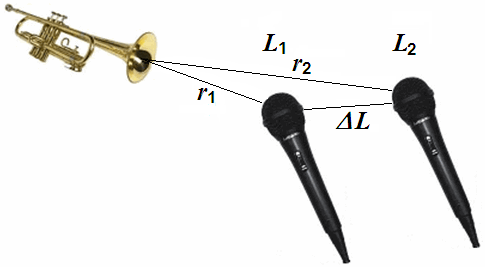Enter the three gray boxes and get the answer in the white box.

Sound is here the sound level in decibels, no matter if it is the sound
pressure level or the sound intensity level – but not the sound power level.

Formulas to calculate the sound level L in dB (sound pressure
level or sound intensity level) in dependence of the distance r.

Sound pressure level (dB) = Sound intensity level (dB)

Sound pressure is not Sound intensity

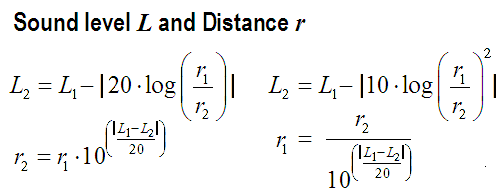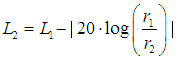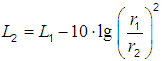Often we talk only of sound level. However, sound pressure as a sound field
quantity is not the same as sound intensity as a sound energy quantity.

Levels of sound pressure and levels of sound intensity decrease equally with the
distance from the sound source with 6 dB per distance doubling. There the
soundpressure drops to a half and the sound intensity to a quarter of the initial
value.

The sound pressure p (amplitude) falls inversely proportional to the distance 1/r
from the sound source. p ~ √ I or p₂ = p₁×(r₁/r₂)
The sound intensity I (energy) falls inversely proportional to the square of the
distance 1/r² from the sound source. I ~ p² or I₂ = I₁×(r₁/r₂)²

Levels of sound pressure and levels of sound intensity measured in decibels
decrease equally with the distance from the sound source.

Sound power or sound power level has nothing to do with the distance from
the sound source.
Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really
always the same 100 watts, which is emitted from the lamp all the time.
Watts don't change with distance.

We consider sound fields in air which are described by the scalar quantity sound
pressure p and the vector quantity v (sound velocity) as a sound field quantity.

The sound level will decrease by 6 dB every time
the source to the listener's distance is doubled.

● For calculations with sound intensities and soundpressures
− that means without level (dB) − go to "Sound and distance".

The sound level depends on the distance between the sound source and the
place of measurement, possibly one ear of a subject.
The sound pressure level L_p in dB without the given distance r to the sound
source is really useless. Unfortunately this error (unknown distance) is quite often.

A doubling of distance from the sound source in the direct field will reduce the "sound level" by
(−)6 dB, no matter whether that are sound pressure levels or sound intensity levels! This will
reduce the sound pressure p (field size) to 1/2 = 0.5 (50 %) and the sound intensity I (energy
size) to 1/2² = 1/4 = 0.25 (25 %) of the initial value.
The inverse distance law 1/r shows the distance performance of field sizes and the
inverse square law 1/r² shows the distance performance of energy sizes.
Squared field sizes are proportional to energy sizes; e.g. p² ~ I

The sound pressure p changes (decrease - drop - fall) with 1/r
over distance. Sound pressure level SPL decreases by (−)6 dB per doubling
of distance from the source to 1/2 = 0.5 (50 %) of the sound pressure initial value.
Sometimes it is said, that the sound pressure p would change with 1/r².
But that is really wrong.

Notice: Intensity and power is not pressure of sound.
Sound energy quantity cannot be sound field quantity.

How is the sound level dependent from the distance to the sound source?
The sound pressure level shows in the free field situation a reduction of 6 dB per
doubling of distance; that means the sound pressure value is a half and not a quarter.

Statement of the distance law:

Distance law for field sizes (source sizes)

Sound level difference: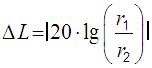
Entfernungsgesetz

Level at far distance: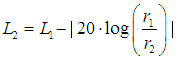
Pressure and distance

Δ L = L₂ − L₁.

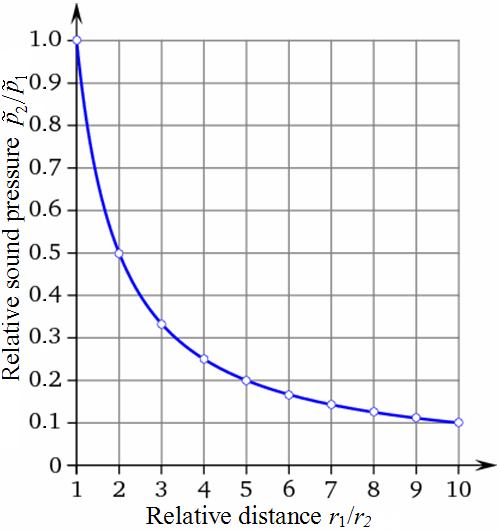
The sound pressure p decreases really with 1/r from the sound source!

In acoustics, the sound pressure of a spherical wave front radiating from
a point source decreases by a ratio of 1/2 as the distance is doubled.
The law is not inverse-square, but is inverse-proportional:

p ~ 1 / r

Calculating sound pressure with the inverse distance law

Relationship of sound intensity I, sound pressure p and the distance law
(r is the distance from the sound source) p ~ 1 / r

From this follows

Where:
p₁ = sound pressure 1 at reference distance r₁ from the sound source
p₂ = sound pressure 2 at another distance r₂ from the sound source

The sound pressure level L_p to plot against
the distance of the sound source r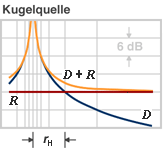
Schallfeld

Kugelwelle = spherical waves
D: direct field of the spheric source
R: reflected field (diffuse field)
r_H: critical distance

Note: The often used term "intensity of sound pressure" is not correct.
Use "magnitude", "strength", "amplitude", or "level" instead.
"Sound intensity" is sound power (acoustic power) per unit area, while
"pressure" is a measure of force per unit area. Intensity (sound energy
quantity) is not equivalent to pressure (sound field quantity). I ~ p²

Since the sound intensity level is difficult to measure, it is common to use
sound pressure level measured in decibels instead. Doubling the sound
pressure raises the Sound Pressure Level SPL with 6 dB.

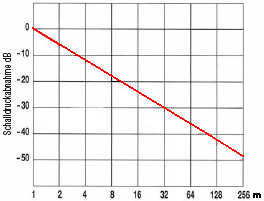
Damping of sound level in decibels with distance

Distance ratio

Computing the additional air damping by air absorption (dissipation) in dependence
on its temperature the relative humidity and the frequency; see: Air damping

Decrease of soundlevel in dB in the direct field with distance.

The sound level decreases with 6 dB per doubling the distance, no matter
if we use the sound pressure level SPL or the sound intensity level SIL.
But that does not work for the sound power level which is emitted constantly
from the sound source.

Conversion of sound units (levels)

For this level damping of sound with distance we have to consider the damping
of air (air damping - dissipation) at larger distances. See:
Absorption of sound by the atmosphere
It is often asked what formula we use for the calculation of air damping:
Formula for calculating the damping of air.

Sound pressure level and Sound pressure

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

Food for thought: If we feel a temperature of 15 degrees Celsius, we
consider the question what is "twice the temperature" of it, as stupid. If we
hear a sound level of 80 dB, the question how much is "twice the volume"
of it, is accepted without formection. Or?

Question: If today we have a temperature of 15 degrees Celsius now,
how warm would it be tomorrow, when it will be twice as hot?

Answer: 0 degrees Celsius is 273 degrees from absolute zero. That is
−273 degrees Celsius equivalent to absolute zero Kelvin. Thus we now
have 273 + 15 = 288 degrees. Twice of it is 576 degrees above absolute
zero of the temperature expected for tomorrow. On the Celsius scale
576 − 273 = 303 degrees Celsius. That's mighty hot!

Decrease in level of sound pressure and sound intensity with distance
Inverse distance law 1/r for sound pressure

The law for sound field quantities
The graphs shown are normalized
Distance ratio	Sound pressure p 1/r
1	1/1 = 1.0000
2	1/2 = 0.5000
3	1/3 = 0.3333
4	1/4 = 0.2500
5	1/5 = 0.2000
6	1/6 = 0.1667
7	1/7 = 0.1429
8	1/8 = 0.1250
9	1/9 = 0.1111
10	1/10 = 0.1000

Conversions and Calculations - Sound sizes and their Levels

Frequently used false statements in the context of
sound values and the distance of the sound source

Correct version	Wrong expression
Sound pressure (amplitude) falls inversely proportional to the distance 1/r from the sound source. That is the 1/r law or the inverse distance law.	Sound pressure (amplitude) falls inversely proportional to the square of the distance 1/r² from the sound source. Really wrong
Sound pressure level decreases by (−)6 dB for doubling of the distance from the source to 1/2 (50 %) of the sound pressure initial value.	Sound pressure level decreases inversely as the the distance increases for doubling of distance from the source by (−)3 dB. wrong
Sound intensity (energy) falls inversely proportional to the square of the distance 1/r² from the sound source. That is the inverse square law 1/r².	Sound intensity (energy) falls inversely proportional to the distance 1/r from the sound source. wrong
Sound intensity level decreases by (−)6 dB for doubling of the distance from the source to 1/4 (25 %) of the sound intensity initial value.	Sound intensity level decreases inversely as the square of the distance increases for doubling of distance from the source by (−)3 dB. wrong

Sound pressure is not intensity

Neither the sound power nor the sound power level decreases in doubling
the distance. Why is this the case?
The sound power level quantifies the totally radiated sound energy from an object.
Different to the sound pressure the sound power is independent of the distance to
the sound source, the surrounding area and other influences.

Changing of sound power with distance is nonsense

Question: How does the sound power decrease with distance"? Answer: "April fool -
The sound power does not decrease (drop) with distance from the sound source."

Levels of sound pressure and levels of sound intensity decrease equally with the
distance from the sound source. Sound power or sound power level has nothing
(!) to do with the distance from the sound source.
Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always
the same 100 watts, which is emitted from the lamp all the time.
Watts don't change with distance.

A frequent question: "Does the sound power depend on distance?" The clear
answer is: "No, not really."

We consider sound fields in air which are described by the scalar quantity sound
pressure p and the vector quantity sound velocity v as a sound field quantity.

Differentiate: Sound pressure p is a "sound field quantity"
and sound intensity I is a "sound energy quantity".
In teachings these terms are not often separated sharply
enough and sometimes are even set equal. But I ~ p².

Sound pressure p and the inverse distance law 1/r

How does an acoustic sound level depend on distance from the source?

Consider a source of sound and imagine a sphere with radius r, centred on the source.
The sound source outputs a total power P, continuously. The sound intensity I is the same
everywhere on this surface of a thought sphere, by definition. The intensity I is defined as the
power P per unit area A. The surface area of the sphere is A = 4 π r², so the sound intensity
passing through each square meter of surface is, by definition:

I = P / 4 π r².

We see that sound intensity is inversely proportional to the square of the distance away.

I₂ / I₁ = r₁² / r₂² or I₂ = I₁ (r₁ / r₂)²

But sound intensity is proportional to the square of the sound pressure, so we could equally
write:

p₂ / p₁ = r₁ / r₂ or p₂ = p₁ (r₁ / r₂)

The sound pressure p changes with 1 / r of the distance.

So, if we double the distance, we reduce the sound pressure by a ratio of 2 and
the sound intensity by a ratio of 4. In other words, we reduce the sound level by
6 dB. If we increase r by a ratio of 10, we decrease the level by 20 dB.

The sound intensity level and the sound pressure levels in dB have the same
value, but the size of sound pressure and the size of acoustic intensity is
different, because I ~ p².

How many decibels (dB) level change is twice (double, half) or three times as loud?

The beginners question is quite simple: How does the sound decrease with distance?
More specifically asked: How does the volume (loudness) decrease with distance?
How does the sound pressure decrease with distance?
How does the sound intensity (not the sound power) decrease with distance?
The power (also the acoustic power) cannot decrease with distance.

Sound pressure and sound power

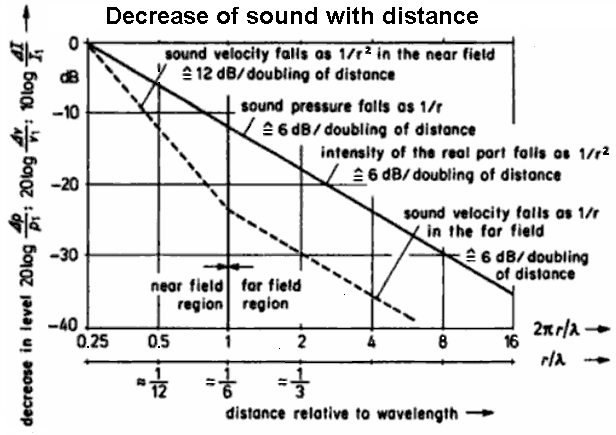Decrease of sound pressure, velocity, and intensity of the sound field
near to and distant from a spherical radiator of the zeroth order

For a spherical wave of a point source we get:
The sound pressure level (SPL) decreases with doubling of distance by (−)6 dB.
The sound pressure falls to 1/2 times (50%) of the initial value of the sound pressure.
The sound pressure decreases with the ratio 1/r to the distance.

For a spherical wave of a point source we get:
The sound intensity level decreases with doubling of distance also by (−)6 dB.
The intensity falls to 1/4 times (25%) of the initial value of the sound intensity.
The sound intensity decreases with the ratio 1/r² to the distance.

For a cylindrical wave that is a line source we get:
The sound pressure level (SPL) decreases with doubling of distance only by (−)3 dB.
The sound pressure falls to 0.707 times (70.7%) of the initial value of the sound pressure.
The sound pressure decreases with the ratio 1/√r to the distance.
*) A loudspeaker line array operates according to this principle, but takes account of the
finite length of the array. Therefore the sound pressure level (SPL) (!) of the low
frequencies decrease (−)6 dB spherically with doubling of the distance.

For a cylindrical wave that is a line source we get:
The sound intensity level decreases with doubling of distance also by (−)3 dB.
The intensity falls to 1/2 times (50%) of the initial value of the sound intensity.
The sound intensity decreases with a ratio 1/r to the distance.

The emitted acoustic power does not decrease with the doubling of distance.
A lamp with the power of 100 watts has in 1 m or in 10 m distance still the same watts.

Inverse distance law
p₂ / p₁= (r₁/ r₂)
Let us take a look at a practical application of this formula: if r₁ = 1 m and at this distance
from the sound source we measure L_p1 = 100 dB at a distance of r₂ = 2 m we will have a
sound pressure equal to: L_p2 = L_p1 – 20 × lg (r₂ / r₁)

Application of the inverse distance formula
L_p2 = 100 − 20 × lg (2 / 1) = 100 − 6.02 = 94 dB_SPL. From this simple example we obtain
an easy, useful rule: every time we move away from a sound source, doubling our
distance from it, the sound pressure level decreases by 6 dB_SPL. Vice versa if we move
closer to the sound source, halving our distance from it, we perceive an increase in sound
pressure of approximately 6 dB_SPL.
This rule is called the inverse distance law.

Question: What is the standard distance to measure sound pressure level away from equipment?
There is no standard distance. It depends on the size of the sound source and the sound pressure level.

Why do some engineers want to use constantly the impractical sound energy sizes,
such as sound intensity and sound power with the reference sound size I₀ = 10⁻¹² W/m²
or P₀ = 10⁻¹² W, when applying the human ear? For noise control calculations that is all right.

Note: The sound pressure level (sound field size) is not to be confused with the sound
power level (sound energy size). The dB values for sound pressure levels are always tied
to the distance to the sound source, whereas the dB values of the sound power level,
logically have no relation to the distance from the sound source. The emitted sound power
of a sound source is independent of location and room independent. It is the same for all
distances from the source. The sound pressure of a sound source is a function of location
and room-dependent. It varies with the distance from the sound
source.

How does the sound decrease with distance?
Sound pressure and sound intensity
The term loudness or volume should here not be
used because it is a psycho-acoustic sensation.

The human perception of loudness - Loudness factor (volume)

The constant unsureness is the answer to the question:
"How many decibels (dB) are doubling a sound"? or "What is twice the sound?"

Answer: Doubling means the "factor 2". What does doubling of a "sound" mean?
Doubling the (sound) intensity is obtained by an increase of the (sound intensity) level of 3 dB.
Doubling the sound pressure is obtained by an increase of the (sound pressure) level of 6 dB.
Doubling the loudness feeling is obtained by an increase of the (loudness) level of about 10 dB.

The question for doubling the decibels (dB) is nonsense!

Simple rule of thumb:
When working with power, 3 dB means douple (twice) the factor and 10 dB means 10-fold.
When working with voltage or current, 6 dB means double (twice) the factor and 20 dB means 10-fold.

In audio, electronics and acoustics use only the word "damping" and not the wrong word "dampening".

"damping" means:
1. a decreasing of the amplitude of an electrical or mechanical wave.
2. an energy-absorbing mechanism or resistance circuit causing this decrease.
3. a reduction in the amplitude of an oscillation or vibration as a result of energy being dissipated as heat.

"dampening" means:
1. To make damp.
2. To deaden, restrain, or depress.
3. To soundproof.

Notice: Damping is energy dissipation and dampening is making something wet.

back

Search Engine

home

Calculation of the sound level L₂, which is found at the distance r₂
Reference distance r₁ from sound source m or ft	Sound level L₁ at reference distance r₁ dBSPL	Search for L₂
Another distance r₂ from sound source m or ft	Sound level L₂ at another distance r₂ dBSPL	Sound level difference Δ L = L₁ − L₂ dB

Calculate the distance r₂, where the sound level L₂ is to find.
Sound level L₁ at reference distance r₁ dBSPL	Reference distance r₁ from sound source m or ft	Search for r₂
Sound level L₂ at another distance r₂ dBSPL	Another distance r₂ from sound source m or ft	Difference of distance Δ r = r₂ − r₁ m or ft


Sound pressure level (SPL) L_p dB-SPL	↔	Sound pressure p Pa = N/m²

Standard reference sound pressure p₀ = 20 μPa = 2 × 10⁻⁵ Pa ≡ 0 dB