Q factor quality factor filter -3 dB band pass BW bandwidth in octaves formula conversion calculation and converter octave width vibration mastering slope dB/oct steepness EQ filter equalizer cutoff freqiency - sengpielaudio
 
Deutsche Version UK-flag s/w - sengpielaudio D-flag - sengpielaudio
 
Bandpass Filter (BPF) and EQ Filter
● Relation between Q  factor and bandwidth  BW ●
 
Calculation
 
Filter conversion: 'bandwidth in octaves' N to quality factor Q
and Q factor to 'bandwidth in octaves' N (octave width)    Q = f0/BW
 
Bandwidth BW = f2 − f1= f0/Q       Equalizer EQ bandpass filter
  Q factor = quality factor   Bandwidth BW of a filter band   f0 = Center frequency
The multiplicative inverse or the reciprocal of the
quality factor 1/Q is called the dissipation factor d (damping)
Often 'Q' and 'bandwidth' are used interchangeably, though they're not. Q is not 1 / N.
Defining the bandwidth as the −3 dB points cannot be correct for a boost gain of 3 dB or less.
 
The Center frequency  f0 is the geometric mean of f1 and f2
f1 and f2 is the cut-off frequency = corner frequency = crossover frequency
= half-power frequency = 3 dB frequency = break frequency.
 
 Bandwidth BW  in octaves N   |   Quality factor Q 
   |   
   ↓  |     ↓
   |   
 Quality factor Q               |   Bandwidth BW  in octaves N 
 
To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

 
Quality factor Q 
 		  ↔  Bandwidth in octaves N 
 
 
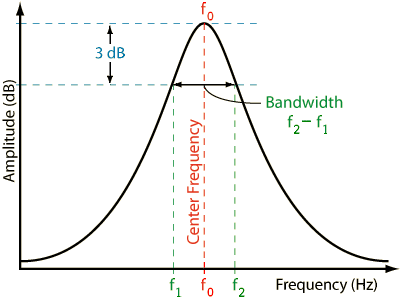Filter resonance

BW = Δf = f0 / Q          Q = f0 / BW          f0= BW × Q = √ (f1 × f2)
BW = f2 − f1            f1 = f02 / f2 = f2 − BW             f2 = f02 / f1 = f1 + BW

Conversion formula: 'octave bandwidth' N to quality factor Q:

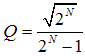Q factor N to Q

Conversion formula: Quality factor Q to 'octave bandwidth' N:

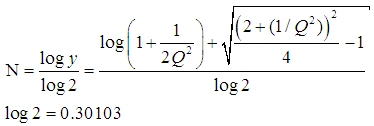Q factor Q to N log

Also known is this longer formula with 4 Qs; see its development at:
Bandwidth in octaves versus Q in bandpass filters − RaneNote 170

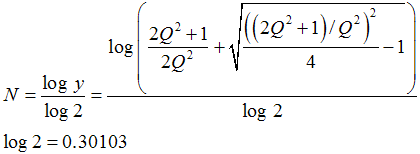Q factor Q to N log

Frequency ratio of an octave:

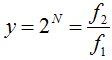Frequency ratio

Formula to convert quality factor Q to 'bandwidth in octaves' N,
but with logarithmus naturalis:

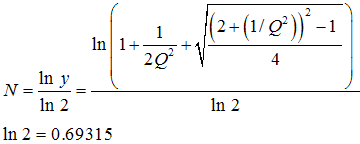Q factor Q to N log

And the very short formula to convert quality factor Q
to 'bandwidth in octaves' N, but with sinh-1 :

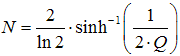Q factor Q to N

The conversion of the bandwidth in response to a different interval than the octave, such as the indication
of the "bandwidth as a function of a fifth" with the interval 2/3 or 1/2 octave is unusual.

Given −3 dB points to find bandwidth BW and quality factor Q.
 BW = f0 / Q             Q = f0 / BW            f0 =√ (f1 × f2)
 
Given bandwidth in octaves N to find quality factor Q.
Q = sqr(2^N) / (2^N − 1)
Given quality factor Q to find bandwidth in octaves N.
N = log(1 + 1 / (2 × Q2) + sqr(((2 + 1 / (Q2))2) / 4 − 1)) / log(2)

The Q Factor
 
Conversion chart or table
'bandwidth in octaves' N to quality factor Q

BW in
octaves		  Filter 
Q		       BW in
octaves		  Filter 
Q		       BW in
octaves		  Filter 
Q		       BW in
octaves		  Filter 
Q
1/80 115.4   1 1.41   4 0.267   7 0.089
1/60 86.6   1 1/4 1.12   4 1/4 0.242   7 1/4 0.082
1/50 72.1   1 1/3 1.04   4 1/3 0.234   7 1/3 0.079
1/40 57.7   1 1/2 0.92   4 1/2 0.220   7 1/2 0.075
1/30 43.3   1 2/3 0.82   4 2/3 0.207   7 2/3 0.071
1/25 36.1   1 3/4 0.78   4 3/4 0.200   7 3/4 0.068
1/20 28.9   2 0.67   5 0.182   8 0.063
1/16 23.1   2 1/4 0.58   5 1/4 0.166   8 1/4 0.058
1/12 17.3   2 1/3 0.56   5 1/3 0.161   8 1/3 0.056
1/10 14.4   2 1/2 0.51   5 1/2 0.152   8 1/2 0.053
1/8 11.5   2 2/3 0.47   5 2/3 0.143   8 2/3 0.050
1/6     8.65   2 3/4 0.45   5 3/4 0.139   8 3/4 0.048
1/5     7.20   3 0.40   6 0.127   9 0.044
1/4     5.76   3 1/4 0.36   6 1/4 0.116   9 1/4 0.041
1/3     4.32   3 1/3 0.35   6 1/3 0.113   9 1/3 0.039
1/2     2.87   3 1/2 0.33   6 1/2 0.106   9 1/2 0.037
2/3     2.14   3 2/3 0.30   6 2/3 0.100   9 2/3 0.035
3/4     1.90   3 3/4 0.29   6 3/4 0.097   9 3/4 0.034
                  10 0.031

Q factor as a function of the bandwidth in octaves N

Bandwidth in
octaves N		 Filter
Q factor
       3.0 wide      0.404 low
2.0 0.667
1.5 0.920
1.0 1.414
2/3 2.145
1/2 2.871
1/3 4.318
1/6 8.651
          1/12 small      17.310 high
 
 
 Notice:
 A low Q factor gives a broad band (wide) bandwidth or 
 a high Q factor gives a narrow band (small) bandwidth. 
  
 
 A high filter quality means narrow-band filtering (notch), with a large Q factor.
 This results in steep filter flanks with a small bandwidth.
 
 A low filter quality means broad-band filtering, with a small Q factor.
 This results in flat filter flanks with a large bandwidth.
 
 The larger the Q the more narrow is the resonance peak.
 The smaller the Q the more broad is the resonance peak.

Notch filters have a large quality factor (Q), corresponding to a small bandwidth.

The Q factor or the bandwidth does
not tell the "steepness" in dB/oct.
 
Slope in dB/oct = steepness of the filter flanks
● Only with high pass and low pass filters − not with bell curves ●
 
Note: The Q factor (quality factor) or the bandwidth is not convertable to the "slope" as dB/oct.
There are mastering equalizers with false information regarding the filter setting as
"Slope in dB/octave" and not Q factor (width), see:
Filter slope or steepness (dB/oct) is not bandwidth = Slope in dB/oct or steepness of filter slopes is not the bandwidth.
 
Given Q factor and center frequency− Find the 3 dB cut-off frequencies
Interrelationship of 'octave bandwidth' N and the quality factor Q
Formulas for conversion of bandwidth in octaves to quality factor
Questions on "Parametric filter adjustment"
Conversion table Q to N and N to Q for parametric filters
Excel conversion − quality factor Q to bandwidth in octaves N
Filter Slope or steepness (dB/oct) is not Bandwidth
Adding decibels of one-third octave bands to level of one octave band
 
With "quality" is not meant how valuable the signal is. It is meant the quality of the filter.
If the filter has flat slopes many frequencies are influenced around the cutoff frequency.
The filter has therefore a larger bandwidth and the so-called quality factor Q is specified as a low number.
If the filter has steep slopes, its bandwidth is smaller. Here a few frequencies below and above its cutoff frequency are affected and the quality factor Q is specified as a high number.
 
Why is the bandwidth and the cutoff frequency found at the level of "−3 dB"?
Why we always take 3 dB down gain of a filter?
Full width at half maximum (FWHM).
Answer: That is the point where the energy (power) is fallen to the value ½ or 0.5 = 50 percent of the initial power as energy quantity, that is equivalent to (−)3 dB = 10×log(0.5). A (−)3 dB power drop is a decrease of 50 % to the value of 50 %.
There the voltage is fallen to the value of √(½) or 0.7071 = 70.71 percent of the initial voltage as field quantity equivalent to (−)3 dB = 20×log(0.7071). A (−)3 dB voltage drop is a decrease of 29.29 % to the value of 70.71 %.
 
(−)3 dB implies ½ the electric power and since the power is proportional to the square of voltage, the value will be 0.7071 or 70.71 % of the passband voltage.
√½ = 1/√2 = √0.5 = 0,7071. P ~ V2, that is 0,5 ~ 0,70712.
 
Sound engineers and sound designers ("ear people") mostly use the usual (sound) field quantity. That's why they say:
The cutoff frequency of a device (microphone, amplifier, loudspeaker) is the frequency at which the output voltage level is decreased to a value of (−)3 dB below the input voltage level (0 dB).
● (−)3 dB corresponds to a factor of √½ = 1/√2 = 0.7071, which is 70.71% of the input voltage.
 
Acousticians and sound protectors ("noise fighters") seem to like more the (sound) energy quantity. They tell us:
The cutoff frequency of a device (microphone, amplifier, loudspeaker) is the frequency at which the output power level is decreased to a value of (−)3 dB below the input power level (0 dB).
● (−)3 dB corresponds to a factor of ½ = 0.5, which is 50% of the input power (half the value).
 
Note: Power gain (power amplification) is not common in audio engineering.
Even power amplifiers for loudspeakers don't amplify the power.
They amplify the audio voltage that moves the voice coil.
 
Sound field quantities    AnimatedLaughingSmiley
Sound pressure, sound or particle velocity, particle displacement or displacement amplitude, (voltage, current, electric resistance).
Inverse Distance Law 1/r		         Sound energy quantities
Sound intensity, sound energy density, sound energy, acoustic  power.
(electrical power).
Inverse Square Law 1/r²
 
Note: A sound field quantity (sound pressure p, electric voltage V) is not a sound energy quantity (sound intensity I, sound power Pak). I ~ p2 or P ~ V2. Sometimes you can hear the statement: The cutoff frequency is there where the level L is decreased by (−)3 dB.
Whatever the user wants to tell us so accurately: Level is level or dB is dB.
 
 
 
back back Search Engine forward home start