

| English version |
| Es gibt keine Lärmabnahme oder Schallverminderung pro Meter. Die Schallpegelabnahme geht mit 6 dB pro Abstandsverdopplung. |
| Die Schallleistung bzw. der Schallleistungspegel haben mit der Entfernung absolut nichts zu tun. Gedankenhilfe: Eine 100 Watt-Glühlampe emittiert ständig die gleiche Leistung. Das ist so - egal ob in 1 m, in 10 m oder selbst in 100 m Abstand. Diese emittierten Watt ändern sich nicht mit der Entfernung (Abstand, Distanz). Die Schallleistung ist die entfernungsunabhängige Ursache während der Schalldruck die entfernungsabhängige Wirkung ist. |
|
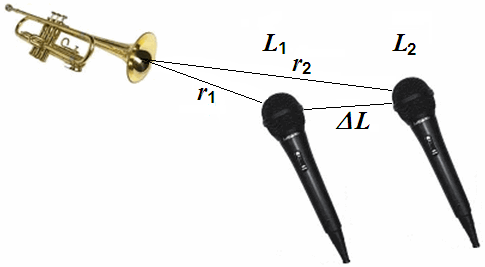
Abnahme (Änderung) des Schalldruckpegels Δ L oder des Schalldrucks p mit der Entfernung r im Freifeld (Direktfeld) − SPL Umrechnung: Entfernungsangaben → Pegeländerung - Das 1/r-Gesetz für Schalldruck Mit Schallpegel (SPL) ist üblicherweise ein logarithmisches Schalldruck-Pegelverhältnis gemeint. |
| Diese Berechnungen sind für Tontechniker gedacht. Es geht um die Entfernung von Punktschallquellen, also von Musikern oder Lautsprechern zum Mikrofon im Direktfeld − d. h. keine Luftdämpfung und Frequenzabhängigkeit z. B. Donner in weiter Entfernung. |
| Vermeide die Verwendung der psychoakustischen Ausdrücke Lautstärke und Lautheit. Diese subjektive Schall-Empfindung ist nicht eindeutig messbar. Die Begriffe "Lautstärke" oder "Lautheit" sind ein Problem, weil diese zur Psycho- Akustik gehören und solch eine persönliche Empfindung nicht klar bestimmbar ist. Lautheit oder Lautstärke wird als psychologische Ergänzung der physischen Schall- Stärke (Amplitude) auch nach anderen Parametern als dem Schalldruck beurteilt, einschließlich der Frequenz, der Bandbreite, der spektralen Zusammensetzung, dem Informationsgehalt, der zeitlichen Struktur, der subjektiven Einstellung, sowie der Einwirkungsdauer des Schallsignals. Der gleiche Schall erzeugt nicht bei allen Individuen (Menschen) die gleiche Lautheitsempfindung. |
| Als psychoakustische Größen zur Beschreibung der "Lautstärke" gibt es den "Lautstärkepegel" (Lautheitspegel) LN mit der Einheit Phon und die "Lautheit" N mit der Einheit Sone. |
| Schallquelle ab (1/r²). Das ist ein häufig erzähltes und gern geglaubtes Märchen. |
 |
| Die Eingabe der Werte in die drei grauen Felder ergibt die Lösung im weißen Feld. Hier geht es beim Schall um den Schallpegel in dB - egal ob Schalldruckpegel oder Schallintensitätspegel, jedoch nicht um den Schallleistungspegel. |
Bei Dezimal-Eingaben ist stets der Punkt zu verwenden
| Formeln zum Berechnen der Schallpegel L in dB (Schalldruckpegel bzw. Schallintensitätspegel) in Abhängigkeit von der Entfernung r. |
 |
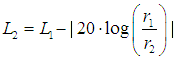 |
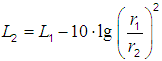 |
| Oft wird einfach nur vom Schallpegel gesprochen. Jedoch ist Schalldruck als Schallfeldgröße nicht das Gleiche wie Schallintensität als Schallenergiegröße. Pegel des Schalldrucks und Pegel der Schallintensität nehmen gleichermaßen mit der Entfernung von der Schallquelle ab - mit 6 dB pro Abstandsverdopplung. Dabei sinkt der Schalldruck auf die Hälfte und die Schallintensität auf ein Viertel des Anfangswerts. Der Schalldruck p (Amplitude) nimmt bei zunehmender Entfernung mit 1/r ab. p ~ √ I oder p2 = p1·(r1/r2) Die Schallintensität I (Energie) nimmt bei zunehmender Entfernung mit 1/r2 ab. I ~ p2 oder I2 = I1·(r1/r2)2 Die Schallleistung oder der Schallleistungspegel haben mit der Entfernung absolut nichts zu tun. Eine 100-Watt-Glühlampe hat in 1 m und in 10 m Entfernung wirklich immer die gleichen 100 Watt, die von der Lampe ständig abgestrahlt (emittiert) wird. Diese Watt ändern sich nicht mit der Entfernung. Vermeide den amateurhaften Begriff Schallstärke. |
| Mit jeder Verdopplung der Entfernung zwischen Schallquelle und Hörer nimmt der Schallpegel um 6 dB ab. |
| Der Pegel des Lärms hängt von der Entfernung zwischen der Schallquelle und dem Ort der Messung, möglicherweise dem Ohr eines Hörers ab. Der Schalldruckpegel Lp in dB ist ohne den genannten Abstand r zur Schallquelle wirklich nutzlos. Leider ist dieser Fehler (unbekannte Entfernung) ziemlich häufig. |
| Sicher verringert eine Verdopplung der Distanz, des Abstands oder der Entfernung von der Schallquelle im Direktfeld den "Schallpegel" immer um (−)6 dB, egal ob es sich um den Schalldruckpegel oder den Schallintensitätspegel handelt! Dabei verringert sich der Schalldruck p (Feldgröße) auf 1/2 = 0,5 (50 %) und die Schallintensität I (Energiegröße) auf 1/22 = 1/4 = 0,25 (25 %) des jeweiligen Anfangswerts. Das reziproke Abstandsgesetz 1/r gilt für das Abstandsverhalten von Feldgrößen und das reziproke Quadratgesetz 1/r2 gilt für das Abstandsverhalten von Energiegrößen. Die Schallfeldgröße zum Quadrat ist proportional der Energiegröße – z. B. p2 ~ I. |
| Der Schalldruck p ändert sich mit dem Abstand 1/r Der Schalldruckpegel nimmt bei Verdopplung des Abstands um (−)6 dB ab, also auf 1/2 (50 %) des Schalldruck-Anfangswerts. Manchmal wird behauptet, der Schalldruck p würde sich mit 1/r2 ändern. Das ist jedoch falsch. Merke: Intensität und Leistung ist nicht Schalldruck. Schallenergiegröße kann nicht Schallfeldgröße sein. |
| Wie ist der Schallpegel von der Entfernung zur Schallquelle abhängig? Der Schallpegel nimmt im Freifeld mit 6 dB pro Abstandsverdopplung ab, das heißt der Schalldruck sinkt dabei auf die Hälfte - und nicht auf ein Viertel. Zur irrigen Meinung, dass der Schall quadratisch mit der Entfernung abnimmt |
| Erklärung des Abstandgesetzes: Abstandsgesetz (Abstandsregel) für Feldgrößen (Quellengrößen) |
Schallpegeländerung: 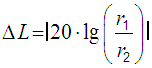 |
Pegel der fernen Quelle: 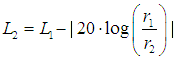 |
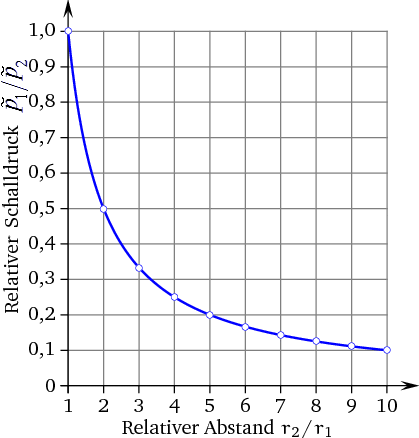
| Schalldruck p gehört zu den Schallfeldgrößen. Der Schalldruck nimmt wirklich mit 1/r von der Schallquelle ab! In der Akustik verringert sich der Schalldruck einer kugelförmigen Wellenfront, die von einer Punktquelle ausgeht um den Faktor von 1/2, wenn der Abstand verdoppelt wird. Die Abnahme geht nicht umgekehrt mit dem "Quadrat", sondern ist umgekehrt proportional zur Distanz: |
p ~ 1 / r
Schalldruckberechnung mit dem reziproken Abstandsgesetz
| Der Zusammenhang von Schallintensität, Schalldruck und Abstandsgesetz: (r ist der Abstand von der Schallquelle zum Messpunkt) p ~ 1 / r |
|
Formeln zur Abstandsdämpfung des Schalldrucks
|
|
|
| Hierbei ist: | ||
| p1 = Schalldruck 1 bei Bezugsabstand r1 von der Schallquelle | ||
| p2 = Schalldruck 2 bei anderem Abstand r2 von der Schallquelle | ||
| Der Schalldruckpegel Lp in Abhängigkeit von der Schallquellenentfernung r im Raum 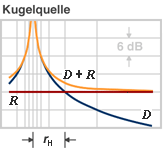 D: Direktschallfeld der Kugelquelle R: Raumschallfeld (Diffusfeld) rH: Hallradius |
| Merke: Die häufig benutzte Bezeichnung "Intensität des Schalldrucks" ist nicht richtig. Für das Wort Intensität ist das Wort "Größe", "Stärke", "Amplitude" oder "Pegel" zu nehmen. "Schallintensität" ist Schallleistung pro Flächeneinheit, während "Druck" ein Maß für Kraft pro Flächeneinheit ist. Intensität als Energiegröße ist niemals Druck als Feldgröße. I ~ p2 |
| Da der Schallintensitätspegel als Schallenergiegröße schwierig zu messen ist, ist es üblich, einfach den Schalldruck als Schallfeldgröße in Dezibel zu messen. Eine Verdopplung des Schalldrucks erhöht den Schalldruckpegel um 6 dB. |
| Abstandsdämpfung in Dezibel |
 |
| Entfernungsverhältnis |
| Berechnen der zusätzlichen Luft-Dämpfung (Dissipation) durch die Luft-Absorption in Abhängigkeit von der Temperatur, der relativen Feuchtigkeit und der Frequenz; siehe: Luft-Dämpfung |
|
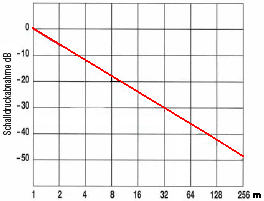
Der Schallpegel nimmt mit 6 dB pro Entfernungsverdopplung ab, egal ob es der Schalldruckpegel SPL oder der Schallintensitätspegel SIL ist. Das gilt jedoch nicht für denSchallleistungspegel, der ständig von der Schallquelle abgestrahlt (emitiert) wird. |
 |
Umrechnung von Schalleinheiten (Pegel)

| Die von einer Schallquelle emittierte Schallleistung ergibt bei freier Schallausbreitung in der Entfernung r1 den Schalldruck p1 bzw. den Schalldruckpegel L1. In der Entfernung r2 ergibt sich der Schalldruck p2 bzw. der Schalldruckpegel L2. Da sich die Schallintensität auf eine immer größer werdende gedachte Kugeloberfläche (proportional r2) verteilt, nimmt die Intensität mit der Entfernung quadratisch ab. Die daraus ableitbare Gesetzmäßigkeit für den Schalldruckpegel lautet 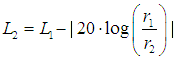 in Dezibel. Das so genannte 6 dB-Gesetz in Dezibel. Das so genannte 6 dB-Gesetzbedeutet, dass der Schalldruckpegel bei Abstandsverdopplung jeweils um 6 dB fällt. Zu dieser Abstandsdämpfung ist bei größeren Entfernungen noch die Dämpfung der Luft (Luftdämpfung) in Betracht zu ziehen; siehe: Berechnung der Luftdämpfung. Häufig wird angefragt, welche Formel hinter der Berechnung der Luftdämpfung steckt: Formel zur Berechnung der Luftdämpfung. |
Schalldruckpegel und Schalldruck
| Einfach den Wert links oder rechts eingeben. Der Rechner arbeitet in beide Richtungen des ↔ Zeichens. |
| Zum Nachdenken: Wenn wir eine Temperatur von 15 Grad Celsius empfinden, halten wir die Frage, wie hoch denn empfindungsmäßig die "doppelte Temperatur" davon sei, für blöd. Wenn wir den Schallpegel von 80 dB empfinden, scheint die Frage, wie hoch denn die "doppelte Lautstärke" davon sei, widerspruchslos hingenommen zu werden. Oder? |
| Frage: Wenn wir heute 15 Grad haben, wie warm müsste es morgen sein, damit es "doppelt" so warm wäre? Antwort: 0 Grad Celsius ist 273 Grad vom absoluten Nullpunkt entfernt. Das heißt −273 Grad Celsius entspricht absolut Null Kelvin. Somit haben wir heute 273 + 15 = 288 Grad. Das Doppelte davon ist 576 Grad vom absoluten Nullpunkt aus gerechnet für die Temperatur von morgen; wobei das damit auf der Celsius-Skala 576 − 273 = 303 Grad Celsius ist. Das ist mächtig heiß! |
 |
|
||||||||||||||||||||||||||||
Häufig vorkommende falsche Behauptungen mit Schallgrößen
im Zusammenhang mit dem Abstand von der Schallquelle.
Falsche Abnahme vom Schalldruck mit der Entfernung zur Schallquelle − ohne Quadrat! p ~ 1 / r
| Richtige Version | Falsche Formulierung |
| Der Schalldruck (Amplitude) nimmt bei zuneh- mender Entfernung von der Schallquelle mit 1/r ab. Das ist das reziproke Abstandsgesetz 1/r. |
Der Schalldruck (Amplitude) nimmt bei zuneh- mender Entfernung umgekehrt proportional mit dem Abstand-Quadrat, also mit 1/r2 ab. Sehr falsch |
| Der Schalldruckpegel nimmt bei Verdopplung des Abstands um (−)6 dB ab, also auf 1/2 (50 %) des Schalldruck-Anfangswerts. |
Der Schalldruckpegel nimmt bei zunehmender Entfernung von der Schallquelle mit (−)3 dB je Abstandsverdopplung ab. falsch |
| Die Schallintensität (Energie) nimmt bei zunehmender Entfernung von der Quelle mit 1/r2 ab. Das ist das reziproke Quadratgesetz 1/r2. |
Die Schallintensität (Energie) nimmt bei zuneh- mender Entfernung von der Schallquelle umgekehrt proportional mit dem Abstand 1/r ab. falsch |
| Der Schallintensitätspegel nimmt bei Verdopplung des Abstands um (−)6 dB ab, also auf 1/4 (25 %) des Intensitäts-Anfangswerts. |
Der Schallintensitätspegel nimmt bei zunehmender Entfernung von der Schallquelle mit (−)3 dB je Abstandsverdopplung ab. falsch |
Schalldruck ist nicht Schallintensität
| Weder die Schallleistung, noch der Schallleistungspegel nimmt bei Verdopplung des Abstands um einen Wert bzw. um irgendwelche dBs ab. Weshalb ist das so? Der Schallleistungspegel quantifiziert die gesamte von einem Objekt als Schall abgestrahlte Energie. Anders als der Schalldruck ist die Schallleistung unabhängig von der Entfernung zum Objekt, dem umgebenden Raum und anderen Einflüssen. |
| Frage: Wie geht denn die Abnahme der Schallleistung mit der Entfernung?" Antwort:" April - April. Die Schalleistung Pak nimmt nicht mit der Entfernung von der Schallquelle ab." Der Schallleistungspegel bzw. die Schallleistung ist fest an die Schallquelle gebunden. Die Schallleistung ist von der Entfernung wirklich unabhängig. Schalldruckpegel und Schallintensiätspegel verringern gleichermaßen mit der Entfernung von der Schallquelle ihren Dezibel-Wert. Jedoch hat die Schallleistung bzw. der Schallleistungspegel nichts (!) mit der Entfernung von der Schallquelle zu tun. Gedankenhilfe: Eine 100-Watt-Glühlampe hat in 1 m und in 10 m Entfernung wirklich immer die gleichen 100 Watt, die von der Lampe ständig abgestrahlt (emittiert) wird. Diese Watt ändern sich nicht mit der Entfernung. Eine häufige Frage: "Ist die Schallleistung entfernungsabhängig oder abstandsabhängig?" Die klare Antwort ist: "Nein, weder noch." |
| Unterscheide: Schalldruck p ist eine "Schallfeldgröße" und Schallintensität I ist eine "Schallenergiegröße". Selten wird dieses in der Lehre scharf genug getrennt und bisweilen sogar unrichtig gleichgesetzt. Aber I ~ p2. |
Schalldruck p und das reziproke Abstandsgesetz 1/r
Wie ist der Schallpegel von der Entfernung zur Schallquelle abhängig?
| Stellen Sie sich eine Schallquelle in der Mitte einer Kugel mit dem Radius r vor. Diese Schallquelle gibt ständig eine Leistung P ab. Die Schallintensität I ist überall auf der Oberfläche der Kugel die gleiche. Die Intensität I ist definiert als die Schallleistung P pro Flächeneinheit A. Die Oberfläche der Kugel beträgt A = 4 π r², so dass die Schallintensität die Schallleistung (Schalleistung) pro Oberfläche in Quadratmeter ist, also per Definition: I = P / 4 π r². Wir sehen, dass die Schallintensität umgekehrt proportional zum Quadrat der Entfernungvon der Quelle ist: I2 / I1 = r1² / r2² oder I2 = I1 (r1 / r2)² Aber die Schallintensität als Energiegröße ist proportional zum Quadrat des Schalldrucks alsFeldgröße. Deshalb können wir schreiben: p2 / p1 = r1 / r2 oder p2 = p1 (r1 / r2) |
| Also der Schalldruck p ändert sich mit dem Abstand 1 / r. Wenn wir also die Entfernung verdoppeln, so reduziert sich der Schalldruck um den Faktor 2, aber die Schallintensität um den Faktor 4. Mit anderen Worten, wir vermindern hierbei den Schallpegel um 6 dB. Wird der Abstand r zur Schallquelle um den Faktor 10 vergrößert, so wird der Pegel um 20 dB vermindert. Der Schallintensitätspegel und der Schalldruckpegel haben den gleichen Wert (Verhältnis) in dB, aber die Größe von Schalldruck und Intensität sind unterschiedlich, denn I ~ p2. |
| Die Anfängerfrage lautet ganz schlicht: Wie nimmt denn der Schall mit der Entfernung ab? Genauer hinterfragt: Wie nimmt die Lautstärke (Lautheit) mit der Entfernung ab? Wie nimmt der Schalldruck mit der Entfernung ab? Wie nimmt die Schallintensität (nicht die Schallleistung) mit der Entfernung ab? Die "Leistung" (auch die Schallleistung) kann nicht mit der Entfernung abnehmen. |
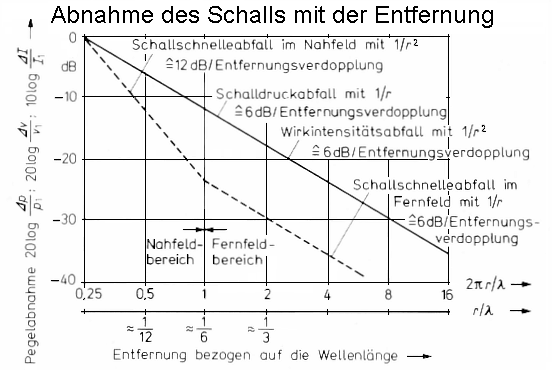 |
| Abnahme von Schalldruck, Schallschnelle und Schallintensiät im Nahfeld und im Fernfeld eines Kugelstrahlers 0. Ordnung |
| Für eine Kugelwelle gilt: Der Schalldruckpegel nimmt bei Verdopplung des Abstands um (−)6 dB ab. Der Schalldruck fällt also auf das 1/2-fache (50 %) des Schalldruckanfangswerts. Der Schalldruck nimmt dabei im Verhältnis 1/r zum Abstand ab. Für eine Kugelwelle gilt: Der Schallintensitätspegel nimmt bei Verdopplung des Abstands auch um (−)6 dB ab. Die Intensität fällt also aufdas 1/4-fache (25 %) des Schallintensitätsanfangswerts. Die Schallintensität nimmt hierbei im Verhältnis 1/r2 zum Abstand ab. Für eine Zylinderwelle also einer Linienquelle gilt: Der Begriff "Zylinderwelle" soll ein reiner Marketing-Ausdruck sein, wird gesagt. Der Schalldruckpegel nimmt bei Verdopplung des Abstands nur um (−)3 dB ab. Der Schalldruck fällt also auf das 0,707-fache (70,7 %) des Schalldruckanfangswerts. Der Schalldruck nimmt dabei im Verhältnis 1/√r zum Abstand ab. *) Ein Lautsprecher Line-Array arbeitet zwar nach diesem Prinzip, jedoch nimmt wegen der endlichen Länge des Arrays der Schalldruckpegel (SPL) (!) der tiefen Frequenzen kugelförmig mit der Verdopplung des Abstands um (−)6 dB ab. Für eine Zylinderwelle also einer Linienquelle gilt: Der Begriff "Zylinderwelle" soll ein reiner Marketing-Ausdruck sein, wird gesagt. Der Schallintensitätspegel nimmt bei Verdopplung des Abstands auch um (−)3 dB ab. Die Intensität fällt also auf das auf 1/2-fache (50 %) des Schallintensitätsanfangswerts. Die Schallintensität nimmt hierbei im Verhältnis 1/r zum Abstand ab. Die emittierte Schallleistung nimmt bei Verdopplung des Abstands überhaupt nicht ab. Gedankenhilfe: Eine 100-Watt-Glühlampe hat in 5 m oder in 10 m Entfernung immer noch die gleichen Watt. Wir betrachten Luftschallfelder, die durch die skalare Größe Schalldruck p und die vektorielle Größe Schallschnelle v als Schallfeldgröße beschrieben werden. |
| Umgekehrtes Abstandsgesetz (Reziprokes Abstandsgesetz) p2 / p1= (r1/ r2) Betrachten wir die praktische Anwendung dieser Formel: Wenn r1 = 1 m ist und wir in dieser Entfernung von der Schallquelle Lp1 = 100 dB messen, dann würden wir im Abstand r2 = 2 m einen Schalldruckpegel von: Lp2 = Lp1 − 20 · lg (r2 / r1) bekommen. Die Anwendung der inversen Abstandsformel Lp2 = 100 − 20 · lg (2 / 1) = 100 − 6.02 = 94 dBSPL. Aus diesem einfachen Beispiel erhalten wir die nützliche Regel: Jedes Mal wenn wir uns von einer Schallquelle auf die doppelte Entfernung begeben, sinkt der Schalldruckpegel um 6 dBSPL. Umgekehrt, wenn wir uns an die Schallquelle annähern, ergibt eine Halbierung der Entfernung eine Schalldruck-Zunahme von etwa 6 dBSPL. Diese Regel heißt reziprokes Abstandsgesetz oder kurz "Abstandsgesetz": |
| Frage: Wie groß ist der Standard-Abstand, um den Schalldruckpegel von einer Schallquelle zu messen? Es gibt keinen genormten Abstand! Er hängt von der Größe der Schallquelle und dem Schallpegel ab. |
| Warum möchten uns die Nicht-Tontechniker beim Anwenden des menschlichen Gehörs ständig die hierbei unpraktischen Schallenergiegrößen, wie Schallintensität und Schallleistung mit der Bezugsschallgröße (Referenz) I0 = 10−12 W/m² bzw. P0 = 10−12 W aufdrängen? Bei Schallschutzberechnungen kann man jedoch nichts dagegen haben. |
| Merke: Der Schalldruckpegel (Schallfeldgröße) ist nicht mit dem Schallleistungspegel (Schallenergiegröße) zu verwechseln.Entfernung (den Abstand) zur Schallquelle gebunden; dagegen haben die dB-Werte beim Schallleistungspegel logischerweise keine Beziehung zum Abstand von der Schallquelle. Die emittierte Schallleistung einer Schallquelle ist ortsunabhängig und raumunabhängig. Sie ist für alle Entfernungen von der Schallquelle gleich. Der Schalldruck einer Schallquelle ist dagegen ortsabhängig und raumabhängig. Er ändert sich mit der Entfernung von der Schallquelle. |
| Wie nimmt der Schall mit der Entfernung ab? Schalldruck und Schallintensität Der Begriff Lautstärke sollte hier als psycho- akustische Empfindung nicht verwendet werden. Das menschliche Lautstärke-Empfinden - Lautheitsfaktor und Lautstärkefaktor |
| Die ständige Unsicherheit bei der Antwort der Frage: "Wie viel dB sind denn doppelter Schall"? Antwort: Verdopplung heißt "Faktor 2". Was soll denn beim "Schall" doppelt sein? Die doppelte (Schall)-Intensität ergibt sich bei einer (Schallintensitäts-)Pegelerhöhung von 3 dB. Der doppelte Schalldruck ergibt sich bei einer (Schalldruck-)Pegelerhöhung von 6 dB. Die doppelte Lautstärkeempfindung ergibt sich bei einer (Lautstärke-)Pegelerhöhung von etwa 10 dB. Die Frage nach doppelten dB (Dezibel) ist unsinnig! |
| Einfache Faustregel: Bei Arbeiten mit Leistung ist 3 dB das Doppelte und 10 dB das 10-fache. Beim Arbeiten mit Spannung oder Strom ist 6 dB das Doppelte und 20 dB das 10-fache. |
| zurück |
Suchmaschine |
Startseite |