

| Deutsche Version |
| Sound waves are nothing more than pressure waves that enable the air and our eardrums to get in motion and let our eardrums and microphones vibrate. That is the sound we hear. Engineers should consider especially the sound pressure and its effect.; see: Sound pressure and Sound power – Effect and Cause Do not use the expression "intensity of sound pressure". Intensity is really not sound pressure. Compare: Sound pressure, sound pressure level, SPL, sound intensity, sound intensity level. How much is a twice (double, half) or three times louder sound? Sound? Which sound? ● For calculations with sound levels (decibels) go to: "Damping of sound levels with distance". How does distance affect sound? No frequency dependance. How do high frequencies affect sound? Frequency dependance. |
 |
| There is no noise decrease or sound drop per meter. We get a sound level drop of 6 dB per doubling of distance. Sound power or sound power level has nothing to do with the distance from the sound source. |
| from the sound source (1/r²). This is an often-told and believed wrong tale. |
| Sound power or sound power level has nothing to do with the distance from the sound source. Thinking helps: A 100 watt light bulb is emitting constantly the same power. That is really the case - no matter if in 1 m, in 10 m, or even in 100 distance. These emitted watts don't change with distance. They stay in the source. Sound power is the distance independent cause of this, whereas sound pressure is the distance-dependent effect. |
|
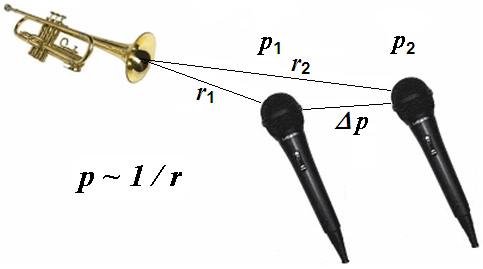
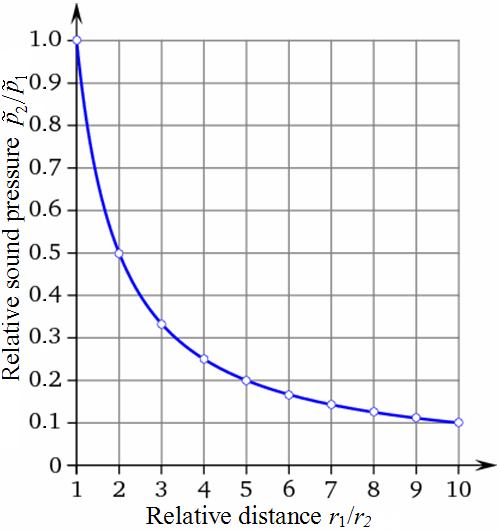
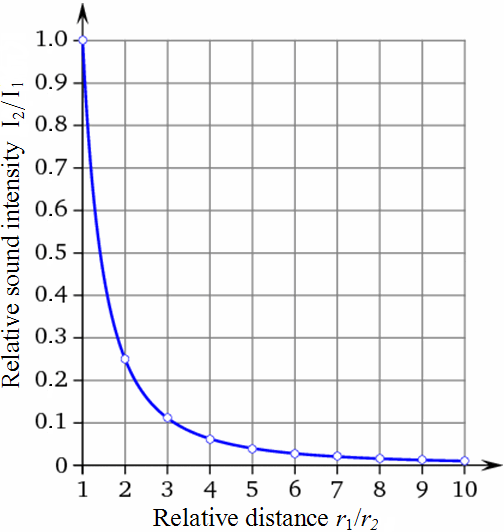
In a direct field or free field, the sound level (SPL) of a spherical wave decreases with doubling of the distance by (−)6 dB. The sound pressure decreases in inverse proportion to the distance, that is, with 1/r from the measuring point to the sound source, so that doubling of the distance decreases the sound pressure to a half (!) of its initial value - not a quarter. The sound intensity decreases inversely proportional to the squared distance, that is, with 1/r² from the measuring point to the sound source, so that doubling of the distance deceases the sound intensity to a quarter of its initial value. Sound pressure (sound field quantity) is not sound intensity (sound energy quantity). I ~ p2. Loudnessis as a psychological correlate of physical strength (amplitude) is also affected by parameters other than sound pressure, including frequency, bandwidth and duration. |
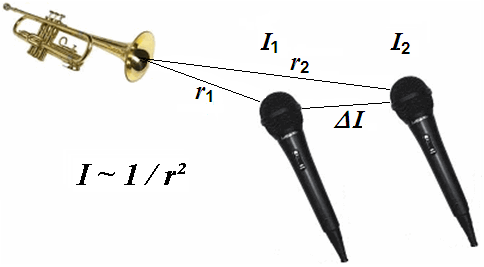 |
| An "unclear" statement: The "sound" decreases with the square of the distance. Which sound exactly? Of course the sound that we hear as particle displacement ξ, sound pressure p, acoustic intensity I, acoustic power Pac, particle velocity v, sound energy density w. Is that really the case? |
| Differentiate: Sound pressure p is a "sound field quantity" and sound intensity I is a "sound energyquantity". In teachings these terms are not often separated sharply enough and sometimes are even set equal. But I ~ p2. The sound power does not decrease with distance. |
| Question: How does the sound power decrease with distance"? Answer: "April fool - The sound power does not decrease (drop) with distance from the sound source." Levels of sound pressure and levels of sound intensity decrease equally with the distance from the sound source. Sound power or sound power level has nothing (!) to do with the distance from the sound source. Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time. Watts don't change with distance. A frequent question: "Does the sound power depend on distance?" The clear answer is: "No, not really." We consider sound fields in air which are described by the scalar quantity p (sound pressure) and the vector quantity v (sound velocity) as a sound field quantity. |
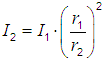 |
| Where: | ||
| p1 | = | sound pressure 1 at reference distance r1 from the sound source |
| p2 | = | sound pressure 2 at the other distance r2 from the sound source |
| I1 | = | sound intensity 1 at reference distance r1 from the sound source |
| I2 | = | sound intensity 2 at the other distance r2 from the sound source |
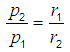 |
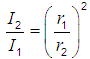 |
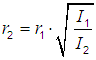 |
| The sound pressure decreases with 1/r at a distance from the sound source. The sound intensity drops with 1/r2 at a distance from the sound source. This is often confused and misunderstood because of the principal difference between the sound pressure as a sound field quantity and the sound intensity as a sound energy quantity is not known. The ear drums of our hearing and also the diaphragms of the microphones are moved effecttively by the sound pressure or the sound pressure level. Sound engineers should considerthis sound pressure as sound field quantity (size) more precisely; see: Sound pressure and Sound power − Effect and Cause |
| Pressure as field quantity is never intensity as energy quantity. |
| Formulas to calculate the sound pressure p or the sound intensity I in dependence of the distance r to a sound source. |
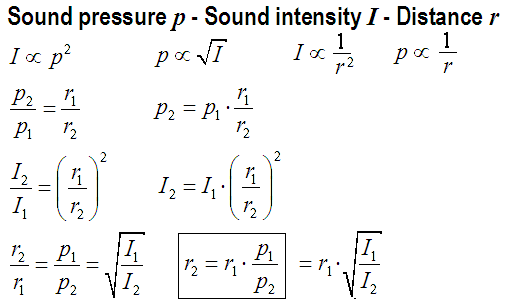 |
 |
|
||||||||||||||||||||||||||||
 |
|
||||||||||||||||||||||||||||
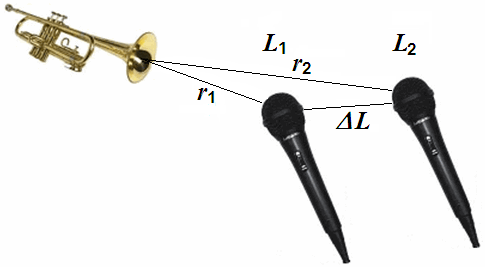 |
| Formulas to calculate the sound level L in dB (sound pressure level or sound intensity level) in dependence of the distance r from a sound source. |
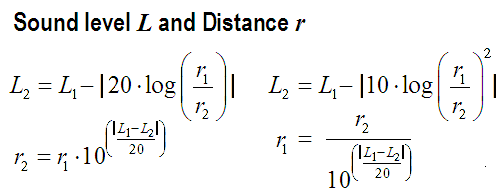 |
| Often we talk only of sound level. However, sound pressure as a sound field
size is not the same as sound intensity as a sound energy size. Levels of sound pressure and levels of sound intensity decrease equally with the distance from the sound source. Sound power or sound power level has nothing (!) to do with the distance from the sound source. Thinking helps: A 100 watt light bulb has in 1 m and in 10 m distance really always the same 100 watts, which is emitted from the lamp all the time. Watts don't change with distance. |
What does sound level mean?
A reduction of the sound power level of the sound source by 6 dB is resulting in a reduction of the sound
pressure level and the sound intensity level at the location of the receiver by also 6 dB, even if the sound
power drops to a factor of 0.25, the sound pressure dropsto a factor of 0.5 and the sound intensity drops
to a factor of 0.25. The reference value for the sound level was chosen so that with a characteristic acoustic
impedance of Z0 = ρ · c = 400 N·s/m3 the sound intensity level results in the same value as the sound
pressure level. We therefore simply speak of the "sound level" and leave it open whether sound pressure
level or sound intensity level is meant.
|
Sound pressure level und sound intensity level
| To use the calculator, simply enter a value. The calculator works in both directions of the ↔ sign. |
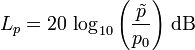 |
Threshold of hearing = Reference sound pressure p0 = 20 μPa = 2 · 10−5 Pa ≡ 0 dB Pa = N/m2
Threshold of hearing = Reference sound intensity I0 = 1 pW/m2 = 10−12 W/m2 ≡ 0 dB
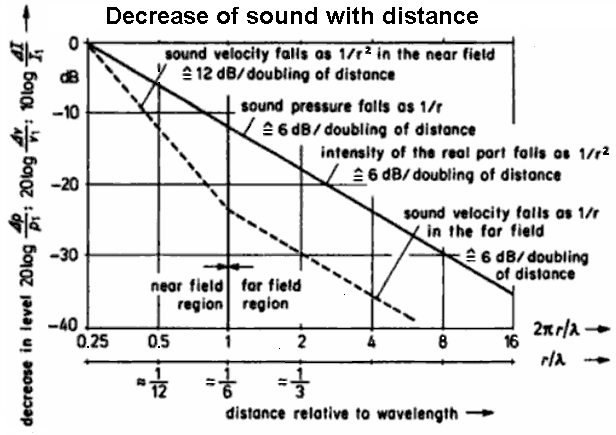 |
| Pressure, velocity, and intensity of the sound field near to and distant from a spherical radiator of the zeroth order |
For a spherical wave: |
| A spherical wavefrontis formed under the assumption of idealized conditions, such as a spherical radiator of zero order (ie, a "breathing" sphere) as a source for radiation in a homogeneous isotropic medium, usually air. For the dropping of sound pressure p and of particle velocity v we get in the far field: (r is the distance from the measurement point to the sound source). 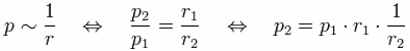 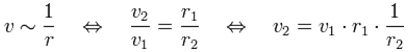 All sound field sizes decrease in the far field after the 6-dB-distance law 1/r. Exception: The sound velocity goes with 1/r² in the near field . That is, the size values are halved by distance doubling. The sound intensity increases as the sound energy size is proportional to the square of the distance from the sound source decreases permanent from the sound source. Since the radiated sound power from the sound source as sound intensity is distributed on a growing area with the distance, the sound intensity falls off in the same proportion as the area grows larger. envelope to the spherical sound source, that is, power is independent of the distance r to the sound source. Sound power Pak in W, sound intensity I in W/m², distance from measuring point r in m, and area A in m². |
| Sound engineers and sound designers ("ear people") are mainly interested
in sound field sizes, and therefore consider the sound pressure drop
at distance doubling. Acousticians and sound protectors ("noise fighters") are mainly interested in sound energy sizes, and therefore consider more the active intensity increase at distance doubling. All persons consider together the same line! If we are a sound engineer to review the sound quality by ear, then think of the soundwaves, which move the eardrums effectively by the sound pressure as sound field size. There is also the advice: Try to avoid to use the words sound power and sound intensity as sound energy sizes. |
|
We do not hear the air pressure changes as such, but the sound pressure at each ear, which is superimposed to the air pressure. |
| In audio, electronics and acoustics use only the word "damping" and not the wrong word "dampening". "damping" means: 1. a decreasing of the amplitude of an electrical or mechanical wave. 2. an energy-absorbing mechanism or resistance circuit causing this decrease. 3. a reduction in the amplitude of an oscillation or vibration as a result of energy being dissipated as heat. "dampening" means: 1. To make damp. 2. To deaden, restrain, or depress. 3. To soundproof. Notice: Damping is energy dissipation and dampening is making something wet. |
| back |
Search Engine |
home |