dB dBu dBFS dBV to volts audio conversion digital - calculator volt to dBu and dBV dB mW SPL dB decibels 0 dBFS - convert dB volt normal decibels relatioship relation explanation analog audio absolute level true rms convertor converter decibel to dbfs converter calculation online attenuation loss gain ratio reference audio engineering sound recording dBFS dBVU 0 dB audio logarithm level converter peak to peak p-p impedance voltage pro consumer audio digital analog recording level

Conversion
Voltage V to Voltage level L_u (dBu) and L_V (dBV)
Voltage level L_u to L_V and Voltage V − Voltage level L_V to L_u and Voltage V

● Decibel (dB) level conversion to volt ●
Level in dBu to dBV, or volts (rms), and dBV to dBu, or volts (rms)
volts (rms) to level in dBu and dBV p-p = peak to peak

Conversion of sound units SPL (levels)
Conversion of factor, ratio, or gain to a level value (gain decibels dB)

The used browser does not support JavaScript.
You will see the program but the function will not work.

Calculator used with kind permission of DoctorProAudio.com
Fill out a gray box above and click the respective 'calculate' bar under it. p-p = peak to peak.
The reference voltage for 0 dBu is 0.775 volt (0.77459667 V) and for 0 dBV it is exactly 1.0 volt.
Scroll down to find the formulas for voltage and power and the calculation of the absolute level.

The origin of the index of dBu comes from "u = unloaded" and dBV comes from "V = 1 volt". Some say:
The "u" in dBu implies that the load impedance is unspecified, unterminated, and is likely to be high.

What is dBu? A logarithmic voltage ratio with a reference voltage of V₀ = 0.7746 volt ≡ 0 dBu
What is dBV? A logarithmic voltage ratio with a reference voltage of V₀ = 1.0000 volt ≡ 0 dBV
The home recording level (consumer audio) of −10 dBV means 0.3162 volts, that is −7.78 dBu.
The studio recording level (pro audio) of +4 dBu means a voltage of 1.228 volts.
The maximum undistorted level of audio amplifiers is +18 dBu. In USA it is +24 dBu.
Domestic gear with a −10 dBV level is usually unbalanced. Studio gear with a +4 dBu level is always balanced. 0 VU = +4 dBu.

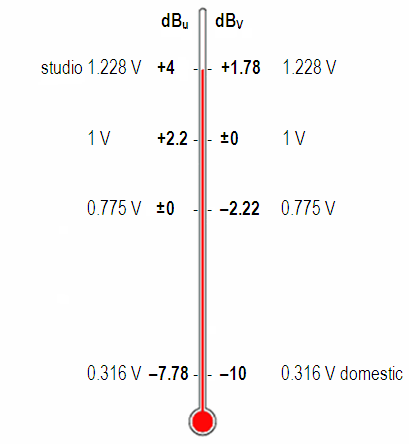
Scale: Level in dBu and dBV in comparison to the voltage in V

	Level dBu	Voltage volt	Level dBV
Studio level international	+4 ●	1.228	+1.78
Standard level 1 Volt	+2.22	1	0 ref.
Standard level 0.775 Volt	0 ref.	0.775	−2.22
Domestic level	−7.78	0.316	−10 ●

The level difference between +4 dBu studio level
and −10 dBV consumer level is Δ L = 11.78 dB (12 dB).

The level difference between dBu level and dBV level is Δ L = 2.2 dB.
0 dBV equals 2.2 dBu or 0 dBu equals −2.2 dBV.

The conversion from level L(dBu) to voltage (volt) is V = 0.775 × 10^(L^/20).
The conversion from voltage V (volt) to level (dBu) is L = 20 × log (V/0.775).

All field quantities, like voltage or sound pressure are
always true RMS values, if not otherwise stated.

In mathematics, the root mean square (abbreviated RMS
or rms), also known as the quadratic mean, is a statistical
measure of the magnitude of a varying quantity.

For sinusodial voltages or currents with ohm's loads
calculations can made easier with RMS = amplitude / √2

Level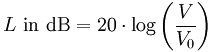

Voltage

Note - Comparing dBSPL and dBA: There is no conversion formula for
measured dBA values to sound pressure level dBSPL or vice versa.
Also you cannot convert "dBA to volts" and vice versa.
Conversion is only possible for measuring one single frequency.

Pro audio equipment often lists an A-weighted noise spec – not
because it correlates well with our hearing – but because it can
"hide" nasty hum components that make for bad noise specs.

Words to bright minds: Always wonder what a manufacturer
is hiding when they use A-weighting. *)

*) http://www.google.com/search?q=Always+wonder+what+a+manufacturer+Rane&filter=0

We don't use the dBm in audio engineering. That belongs to power, we don't need here.

If you really need dBm with "m = 1 milliwatt or one thousandth (10⁻³) of a watt", go to:
The dBm calculator and power matching or impedance matching

Explanation: What is "dBFS"? (Digital Audio)

dBFS - Digital recording level

Analog levels and digital levels are different realms.

♦ An often posted question: "Please, can you help me convert from dBFS to dBu".
Never express analog signal levels in terms of dBFS.
Follow this and you will not confuse anyone.

There is no decibel to dBFS converter
Notice - Comparing dBu and dBFS: There is really no fixed
world standard like e.g. −20 dBFS = +4 dBu = 0dBVU.
The digital peak scale is not equivalent to the analog RMS scale.

You can never match dBFS and dBu.

dBu is volts - you measure it with a volt meter.
Analog audio: positive and negative voltage.

dBFS is in contrast a binary number.
Digital audio: zeroes and ones.

There is no such thing as peak volts dBu *)

It is incorrect to state peak voltage levels in dBu.

*) http://www.rane.com/note169.html
*) http://www.rane.com/pdf/ranenotes/No_Such_Thing_as_Peak_Volts_dBu.pdf

dBFS must have a minus sign at the beginning. There is not something like +6 dBFS.

There is no such standardized reference. x dBFS is a digital voltage level
(peak) and y dBVU or dBu is an analog voltage level (RMS).

Digital and analogue are two totally different realms.

That's why there is no relation between dBFS and dBVU or dBu, whatsoever.
Analog meter (ppm): attack time 10 to 300 ms − reading rms values.
Digital meter: attack time < 1 ms − reading peak values. That is really some
difference.

Advice: Watch only your digital meters and go up to 0 dBFS, but never go
over this mark. We use "headroom" in the analog domain. That is OK, but
we don't need digital "headroom" as an always "unused" forbidden
zone.
You are free to choose your private headroom, if you like that, but there is no
standard that you have to do that.
The demand for a high modulation level, stand in the contrary to the claim,
to avoid overloading.

Never take the following funny guessing game for granted. Use it only as a rough guide:
European & UK calibration for Post & Film is −18 dBFS = 0 VU = +4 dBu

BBC spec: −18 dBFS = PPM "4" = 0 dBu
American Post: −20 dBFS = 0 VU = +4 dBu
Orchestral −18 dBFS = 0 VU = +4 dBu
Rock and / or Radio −16, or −14, or −12 dBFS = 0 VU = +4 dBu
Digi 002 is only capable of −14 dBFS.
German ARD & studio PPM +6 dBu = −10 (−9) dBFS. +16 (+15) dBu = 0 dBFS. No VU.
• EBU R68-2000 - The European Broadcasting Union recommends: digital level
−9 dBFs (maximum). You have to keep the upper 9 dBs empty without any use.
The reference level is −18 dBFs. 0 dBFs is equal to +15 dBu.
Notice: 0 dBFS is the permitted maximum digital level.

The EBU broadcasters have a problem, because they want to use the old slow meters with the
dBu scale (attack 10 ms, quasi-peak) of the analog times for digital recordings.
The rest of the world looks always at the fast digital meters (attack < 1 ms, peak) with the dBFS
scale. Forget looking at the dBu scale of the meters.
It seems to come a change from QPPM-modulation to loudness (ITU/EBU) and true-peak.
Look at: EBU R 128.

Note: The guidelines of the EBU to set the maximum gain
to −9 dB dBFS should not apply if not working for the
European Broadcasting Union. Whose maximum levels
of digital CD masters are −9dBFS, should not be
surprised if the CDs are not loud enough.
9 dB up to the top are left free with really no use.

More readable papers of the topic "Loudness and Level":

10 things you need to know about ... EBU R 128 - the EBU loudness recommendation

Florian Camerer: Loudness On the way to nirvana - audio levelling with EBU R 128

LUFS = Loudness Units relative to Full Scale

The formulas for voltage and power
and the calculation of the absolute level

To use the calculator, simply enter a value.
The calculator works in both directions of the ↔ sign.

dBm indicates that the reference power is P₀ = 1 milliwatt = 0.001 watt ≡ 0 dB

Conversion of voltage or power ratios to decibels dB - table and chart

Table of Sound Pressure Levels and Corresponding Sound Pressure and Sound Intensity

RMS voltage, peak voltage and peak-to-peak voltage

The parameters of the mains or "power" sine wave form are summarized at the table below:

Average voltage	RMS voltage (V_RMS)	Peak voltage (V_p) = (Û)	Peak-to-peak voltage (V_pp)
0 volts	117 volts = V_RMS = ~V	165 volts = √2×V_RMS = 0,5 × V_pp	330 volts = 2×√2×V_RMS = 2 × V_p
0 volts	230 volts = V_RMS = ~V	325 volts = √2×V_RMS = 0,5 × V_pp	650 volts = 2×√2×V_RMS = 2 × V_p

The value V_RMS of an alternating voltage V (t) = V₀ × f(t)is defined so that the
effective DC power corresponds V_RMS² / R = V_RMS × I_RMS to an ohmic resistance
of the middle resistive power of this AC voltage to the same resistance.

The crest factor means the ratio of the peak voltage to the RMS voltage.
If you need to calculate an attenuator (attenuation calculation) you calculate a voltage divider.

Voltage conversions

Voltage	V_RMS = ~V	V_p	V_pp
Average voltage RMS V_RMS =	−	0.7071 × V_p	0.3535 × V_pp
Peak voltage V_p =	1.414 × V_RMS	−	0.5000 × V_pp
Peak-to-peak voltage V_pp =	2.828 × V_RMS	2.000 × V_p	−

Different voltage levels

Level	Level L in dB	Voltage RMS	Voltage peak-to-peak
European studio level - ARD broadcast level	+6 dBu	1.55 V	4.38 V
International studio level - USA	+4 dBu	1.228 V	3.47 V
Domestic recording (Consumer units)	−10 dBV	0.3162 V ≡ −7.78 dBu	0.894 V
Sound pressure level (auditory threshold)	0 dB	2×10⁻⁵ Pa ≡ 0 dBSPL	5.66×10⁻⁵ Pa
Reference studio level re 0.775 volt	0 dBu	0.7746 V	2.19 V
Reference studio level re 1 volt	0 dBV	1.0000 V	2.828 V

International reference values

Physical unit	Level unit	Reference value	Note
Voltage	V₀ = 0.775 V	≡ 0 dBu	Audio engineering, no impedance reference!
Voltage	V₀ = 1 V	≡ 0 dBV	Audio engineering, USA
Voltage	V₀ = 1×10⁻⁶ V		HF receiver and amplifier technology
Voltage	V₀ = 0.224 V		HF technology - Reference 1 mW at Z = 50 Ω
Voltage	V = 1.228 V		Studio level +4 dBu, USA - Reference 0.7746 V
Voltage	V = 1.55 V		Studio level +6 dBu, ARD - Reference 0.7746 V
Voltage	V = 0.3162 V		Home recording level −10 dBV - Reference 1.0 V ≡ −7.78 dBu
Sound pressure	p₀ = 2×10⁻⁵ Pa	≡ 0 dB	Sound Pressure Level SPL, auditory threshold (Sound field size)
Sound particle velocity	v₀ = 5×10⁻⁸ m/s	≡ 0 dB
Sound intensity	I₀ = 1×10⁻¹² W/m²	≡ 0 dB	Threshold of pain at 1 W/m² (Sound energy size)
Power	P₀ = 1 W	≡ 0 dBW	The reference impedance must always be told
Power	P₀ = 1 mW	≡ 0 dBm	Z = 600 Ω (telephones) or Z = 50 Ω (antennas)
Electric field strength	E₀ = 1×10⁻⁶ V/m

Decibels (dB) Calculator

Decibels are defined as ten times the log of a power ratio. Decibels convert
multiplication and division calculations into simple addition and subtraction operations.

This calculator converts between decibels, voltage gain (or current), and power gain.
Just fill in one field and the calculator will convert the other two fields.

Equations: Level in dB: L = 20 × log (V₁/V₂) = 10 × log (P₁/P₂)

The dBm is a logarithmic measure of power compared to 1 mW,
that means it is power dependent.
It can be converted to a voltage, if the load impedance is known.
Typically the impedance (load) is 600 ohms.

Equation: Level in dBm: L_P = 10 × log (P / 0.001)

Simple rule of thumb: When working with power: 3 dB is twice, 10 dB is 10 times.
When working with voltage or current: 6 dB is twice, 20 dB is 10 times.

Why is the bandwidth and the cutoff frequency found at the level of "−3 dB"?
Why we always take 3 dB down gain of a filter?
Full width at half maximum (FWHM).
Answer: That is the point where the energy (power) is fallen to the value ½ or 0.5 = 50 percent of the initial power as energy
quantity, that is equivalent to (−)3 dB = 10×log(0.5). A (−)3 dB power drop is a decrease of 50 % to the value of 50%.
There the voltage is fallen to the value of √(½) or 0.7071 = 70.71 percent of the initial voltage as field quantity equivalent to
(−)3 dB = 20×log(0.7071). A (−)3 dB voltage drop is a decrease of 29.29 % to the value of 70.71 %.

(−)3 dB implies ½ the electric power and since the power is proportional to the
square of voltage, the value will be 0.7071 or 70.71 % of the passband voltage.
√½ = 1/√2 = √0,5 = 0,7071. P ~ V², that is 0,5 ~ 0,7071².

Sound engineers and sound designers ("ear people") mostly use the usual (sound) field quantity. That'swhy they say:
The cutoff frequency of a device (microphone, amplifier, loudspeaker) is the frequency at which the output voltage level
is decreased to a value of (−)3 dB below the input voltage level (0 dB).
● (−)3 dB corresponds to a factor of √½ = 1/√2 = 0.7071, which is 70.71% of the input voltage.

Acousticians and sound protectors ("noise fighters") seem to like more the (sound) energy quantity. They tell us:
The cutoff frequency of a device (microphone, amplifier, loudspeaker) is the frequency at which the output power level is
decreased to a value of (−)3 dB below the input power level (0 dB).
● (−)3 dB corresponds to a factor of ½ = 0.5, which is 50% of the input power (half the value)..

Note: Power gain (power amplification) is not common in audio engineering.
Even power amplifiers for loudspeakers don't amplify the power.
They amplify the audio voltage that moves the voice coil.

Sound field quantities

Sound pressure, sound or particle velocity,
particle displacement or displacement amplitude,
(voltage, current, electric resistance).
Inverse Distance Law 1/r

Sound energy quantities
Sound intensity, sound energy density,
sound energy, acoustic power.
(electrical power).
Inverse Square Law 1/r²

Note: A sound field quantity (sound pressure p, electric voltage V) is not a sound energy
quantity (sound intensity I, sound power P_ak). I ~ p² or P ~ V². Sometimes you can hear
the statement: The cutoff frequency is there where the level L is decreased by (−)3 dB.
Whatever the user wants to tell us so accurately: Level is level or dB is dB.

back

Search Engine

home

Voltage V volts	↔	Voltage level L_V dBV
$V = V_0 \cdot 10^\frac{L_V}{20} \ \mbox{volts}$		$L_V = 20\, \log_{10}\left(\frac{V}{V_0}\right) \ \mbox{dBV}$
Reference voltage V₀ = 1 Volt ≡ 0 dBV

Voltage V (audio) volts	↔	Voltage level L_U (audio) dBu
$V = V_0 \cdot 10^\frac{L_V}{20} \ \mbox{volts}$		$L_V = 20\, \log_{10}\left(\frac{V}{V_0}\right) \ \mbox{dBu}$
Reference voltage V₀ = 0.7746 Volt ≡ 0 dBu

Electric power P watts	↔	Electric power level L_P dB

Reference electric power P₀ = 1 W ≡ 0 dB

Electric power P (telephone) watts	↔	Electric power level L_P dB_m

Reference power P₀ = 1 milliwatt (mW) = 0.001 W ≡ 0 dB_m

Impedance = ohms
dBm	Power (watts)	Voltage RMS	V_p of sinusoid