

| Deutsche Version |
| To perceive sound means spatial hearing. Sound is either useful or useless. Desired sound is information and pleasing to us. Unwanted sound is noise (ambient noise or background noise). Often it is difficult to decide whether a sound is information or noise. |
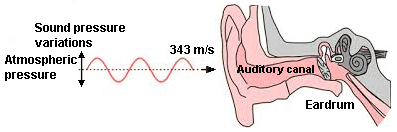
Sound waves move our eardrums (tympanic membranes).
But which sound quantity produces this effect?
 |
|
Sound pressure and Sound power – Effect and Cause Sound power is the cause - but sound pressure produces the audible effect. |
| Sound pressure p in Pa or N/m Sound intensity (acoustic intensity) I in W/m² Acoustic impedance Z = ρ0 × c in N·s/m³ or Pa·s/m Sound levels Lp = 20 × log (p / p0) = LI = 10 × log (I / I0) = 10 × log (p² / p0²) in dB The dB scale in dB Reference values p0, I0 |
| Sound pressure Sound waves are pressure fluctuations, compression and rarefaction of the molecules in the medium through sound waves propagate. The unit for sound pressure is pascal (Pa), equal to newton per square metre (N/m²). The sound pressure may be measured with a pressure sensitive device such as a microphone (for measurements in air) or a hydrophone (for measurements in water). Sound intensity and sound pressure, p, in a plane wave are related through the equation: I = p² / (ρ0 × c) in Watt/m², ρ0 × c = Z0 as characteristic acoustic impedance where ρ0 is the specific density of the medium through which the sound propagates. c is the propagation speed of sound in the medium. The instantaneous particle velocity, v, of a sound wave within the plane wave can be related to the sound pressure, p, through the equation: v = p / (ρ0 × c) in metre/second. The displacement amplitude ξ (xi), or particle motion, of a sound wave can be related to its sound pressure and frequency through the equation: ξ = p / (ω × ρ0 × c) in metre (RMS), where ω = 2π × f is the angular frequency, and f is the frequency of the wave. The above formulae hold for both plane and spherical waves when the distance to the sound source is more than a wavelength at the lowest frequency, called the far field. The sound pressure that represents the lowest limit of human hearing is 20 μPa, corresponding to a sound intensity of 10−12 Watt/m², will cause a displacement of the eardrum that is in the order of 10−9 centimetres at a frequency of 1000 Hz. This is approximately one-tenth the diameter of a hydrogen molecule. Sound intensity The sound intensity (acoustic intensity), I, of a sound wave is defined as the average rate of flow of energy through a unit area normal to the direction of wave propagation. The unit for sound intensity is watts per square metre (W/m²), which can also be expressed as joules per second per square metre (J/s/m²). In some cases it has been stated that the loudness of the sound is determined by its sound intensity. This is not true in the general case, for loudness and (sound) intensity are not synonymous. The loudness of a sound is subjective, and the loudness is in all cases a sensed combined function of both sound intensity and frequency. Acoustic impedance The factor ρ0 × c is called the acoustic impedance Z0, and describes the conditions for sound propagation through the medium. ρ (rho) = density, c = speed of sound, and v = sound particle velocity. The unit for acoustic impedance Z0 is N·s/m³. As seen above, the acoustic impedance Z0 is the ratio between the sound pressure and the instantaneous particle velocity: Z0 = ρ0 × c = p / v. The acoustic impedance is an important factor in all evaluations of sound waves, especially when comparing sound measurements in air and in water. For such evaluations, it is customary to specify the characteristic acoustic impedance Z0 as follows: Air: Z0 = 413 N·s/m³ or Pa·s/m at the temperature of ϑ (theta) = 20°C at standard atmospheric pressure. Water: Z0 = 1 480 000 N·s/m³ (distilled water at 20°C). The similarity between ohm’s law for electrical computations and the above equations is a useful consideration for the understanding of acoustic calculations, where sound intensity is equivalent to power (watt), sound pressure is equivalent to voltage (volt) and sound impedance is equivalent to resistance (ohm), see: "The Formula Wheel of Acoustics" Sound levels The definition of sound level is not directly given by mathematical equations, but depends on a number of factors, including the strength of the sound wave, the frequency and the length of the sound exposure, and whether the sound is propagating in the medium of air or water. The dB scale Due to the wide range of pressures and intensities encountered in measurements of sound, it is customary to describe these through the use of a logarithmic scale. The most generally used logarithmic is the scale for describing sound is the decibel scale (dB). The absolute sound intensity level, LI, of a sound intensity, I, is defined as: LI = 10 × log (I / I0) in dB, where I is the measured sound intensity in W/m² (watts per square meter), and the reference sound intensity is I0 = 1 pW/m² = 10−12 W/m². Notice: log is the logarithm to the base 10. Since sound intensity is proportional to sound pressure squared, the decibel expression for the absolute sound pressure level becomes: Lp or SPL = 10 × log (p² / p0²) = 20 × log (p / p0) in dB, where p is the measured sound pressure in Pa (pascal) or N/m², and the reference sound pressure is p0 = 0.00002 Pa = 20 µPa = 20 × 10−6 Pa = 2 × 10−5 Pa. It is important to note that the decibel scale is a relative measure, and no "unit" for measuring sound. Therefore other units of measurement and reference level can be used instead of the standards indicated above. Reference values As reference for sound pressure of p0 or sound intensity I0, different values are used for measurements in air and in water. For measurements of sound in air, the reference sound pressure is set as: p0 (air) = 20 µPa = 0.00002 Pa = 2 × 10−5 Pa (0.0002 μbar) as effective (root-mean square) and the reference sound intensity is I0 = 10−12 Watt/m². This corresponds to the lower limit of the sensation of human hearing at 1000 Hz, equivalent to 0 dB. For measurements of sound in water (underwater sound), the reference sound pressure is set as: p0 (water) = 1 μPa = 0.000001 Pa = 10−6 Pa (0.00001 μbar), also equivalent to 0 dB. It is important to note the different reference values between measurements made in air and in water. The difference between the two is 26 dB. Given a dB value, there is no standard nomenclature that will say whether a measurement is made in air or in water. Therefore, any reference to a dB value must be carefully checked in order to determine where the measurement is taken, and what reference level is used. There is a physical difference between sound in air and in water, and a different reference level is used. Therefore, in comparison of sound pressure measurements made in air and in water, a correction factor of 62 dB must be added to the air measurements. |
| back |
Search Engine |
home |